An Enigma machine with its wheels, lamps and plugboard exposed. Once the operator had inserted the correct wheels for the day, he closed the inner lid.4

The Tunny radio network of the German Army,
March 1943 – July 1944.7


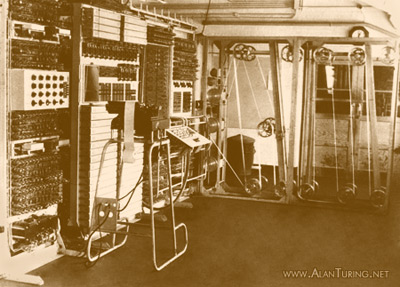
Tunny with its twelve encoding wheels exposed.9
Colossus, the first large-scale electronic computer, was used against the German system of teleprinter encryption known at Bletchley Park as ‘Tunny’. Technologically more sophisticated than Enigma, Tunny carried the highest grade of intelligence. From 1941 Hitler and the German High Command relied increasingly on Tunny to protect their communications with Army Group commanders across Europe.
Tunny messages sent by radio were first intercepted by the British in June 1941. After a year-long struggle with the new cipher, Bletchley Park first read current Tunny traffic in July 1942. Tunny decrypts contained intelligence that changed the course of the war in Europe, saving an incalculable number of lives.
The Tunny machine was manufactured by the German Lorenz company.1 The first model bore the designation SZ40, ‘SZ’ standing for ‘Schlüsselzusatz’ (‘cipher attachment’). A later version, the SZ42A, was introduced in February 1943, followed by the SZ42B in June 1944. ‘40’ and ‘42’ appear to refer to years, as in ‘Windows 97’.
Tunny was one of three types of teleprinter cipher machine used by the Germans. (The North American term for ‘teleprinter’ is ‘teletypewriter’.) At Bletchley Park (B.P.) these were given the general cover name ‘Fish’. The other members of the Fish family were Sturgeon, the Siemens and Halske T52 Schlüsselfernschreibmaschine (‘Cipher Teleprinter Machine’),2 and the unbreakable Thrasher.3 Thrasher was probably the Siemens T43, a one time tape machine. It was upon Tunny that B.P. chiefly focussed.
The Tunny machine, which measured 19" by 15½" by 17" high, was a cipher attachment. Attached to a teleprinter, it automatically encrypted the outgoing stream of pulses produced by the teleprinter, or automatically decrypted incoming messages before they were printed. (Sturgeon, on the other hand, was not an attachment but a combined teleprinter and cipher machine.) At the sending end of a Tunny link, the operator typed plain language (the ‘plaintext’ of the message) at the teleprinter keyboard, and at the receiving end the plaintext was printed out automatically by another teleprinter (usually onto paper strip, resembling a telegram). The transmitted ‘ciphertext’ (the encrypted form of the message) was not seen by the German operators. With the machine in ‘auto’ mode, many long messages could be sent one after another—the plaintext was fed into the teleprinter equipment on pre-punched paper tape and was encrypted and broadcast at high speed. Enigma was clumsy by comparison. A cipher clerk typed the plaintext at the keyboard of an Enigma machine while an assistant painstakingly noted down the letters of the ciphertext as they appeared one by one at the machine’s lamp-board. A radio operator then transmitted the ciphertext in the form of Morse code. Morse code was not used with Tunny: the output of the Tunny machine, encrypted teleprinter code, went directly to air.4
International teleprinter code assigns a pattern of five pulses and pauses to each character. Using the Bletchley convention of representing a pulse by a cross and no pulse by a dot, the letter C, for example, is •xxx•: no-pulse, pulse, pulse, pulse, no-pulse. More examples: O is •••xx, L is •x••x, U is xxx••, and S is x•x••. (The complete teleprinter alphabet is shown in Appendix 1: The teleprinter alphabet.) When a message in teleprinter code is placed on paper tape, each letter (or other keyboard character) takes the form of a pattern of holes punched across the width of the tape. A hole corresponds to a pulse (cross).
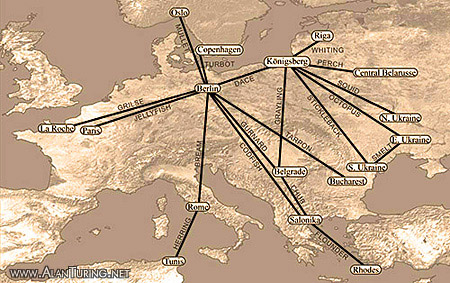
The first Tunny radio link, between Berlin and Athens/Salonika, went into operation on an experimental basis in June 1941.5 In October 1942 this experimental link closed down, and for a short time it was thought that the Germans had abandoned the Tunny machine.6 Later that same month Tunny reappeared in an altered form, on a link between Berlin and Salonika and on a new link between Königsberg and South Russia.7 At the time of the allied invasion in 1944, when the Tunny system had reached its most stable and widespread state,8 there were 26 different links known to the British.9 B.P. gave each link a piscine name: Berlin-Paris was Jellyfish, Berlin-Rome was Bream, Berlin-Copenhagen Turbot (see right-hand column). The two central exchanges for Tunny traffic were Strausberg near Berlin for the Western links, and Königsberg for the Eastern links into Russia.10 In July 1944, the Königsberg exchange closed and a new hub was established for the Eastern links at Golssen, about 20 miles from the Wehrmacht’s underground command headquarters south of Berlin. During the final stages of the war, the Tunny network became increasingly disorganised.11 By the time of the German surrender, the central exchange had been transported from Berlin to Salzburg in Austria.12
There were also fixed exchanges at some other large centres, such as Paris.13 Otherwise, the distant ends of the links were mobile. Each mobile Tunny unit consisted of two trucks.14 One carried the radio equipment, which had to be kept well away from teleprinters for fear of interference. The other carried the teleprinter equipment and two Tunny machines, one for sending and one for receiving. This truck also carried a device for punching tapes for auto transmission. Sometimes a land line was used in preference to radio.15 In this case, the truck carrying the Tunnies was connected up directly to the telephone system. (Only Tunny traffic sent by radio was intercepted by the British.)
As with the Enigma, the heart of the Tunny machine was a system of wheels (see right-hand column). Some or all of the wheels moved each time the operator typed a character at the teleprinter keyboard (or in the case of an ‘auto’ transmission from a pre-punched tape, each time a new letter was read in from the tape). There were twelve wheels in all. They stood side by side in a single row, like plates in a dish rack. As in the case of Enigma, the rim of each wheel was marked with numbers, visible to the operator through a window, and somewhat like the numbers on the rotating parts of a combination lock.
From October 1942 the operating procedure was this. Before starting to send a message, the operator would use his thumb to turn the wheels to a combination that he looked up in a codebook containing one hundred or more combinations (known as the QEP book). At B.P. this combination was called the setting for that particular message. The wheels were supposed to be turned to a new setting at the start of each new message (although because of operator error this did not always occur). The operator at the receiving end, who had the same QEP book, set the wheels of his Tunny machine to the same combination, enabling his machine to decrypt the message automatically as it was received. Once all the combinations in a QEP book had been used it was replaced by a new one.
|
|
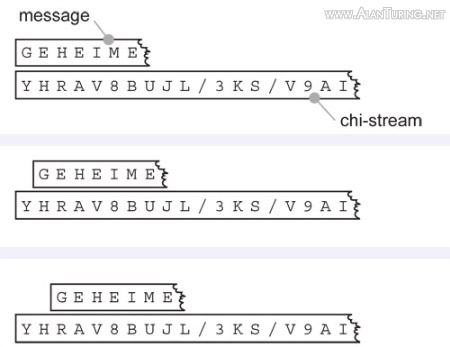
The Tunny machine encrypted each letter of the message by adding another letter to it. (The process of adding letters together is explained in the next paragraph.) The internal mechanism of the Tunny machine produced its own stream of letters, known at B.P. as the ‘key-stream’, or simply key. Each letter of the ciphertext was produced by adding a letter from the key-stream to the corresponding letter of the plaintext.
The Tunny machine adds letters by adding the individual dots and crosses that compose them. The rules that the makers of the machine selected for dot-and-cross addition are simple. Dot plus dot is dot. Cross plus cross is dot. Dot plus cross is cross. Cross plus dot is cross. In short, adding two sames produces dot, and adding a mixed pair produces cross. (Computer literati will recognise Tunny addition as boolean XOR.)
For example, if the first letter of the plaintext happens to be M, and the first letter of the key-stream happens to be N, then the first letter of the ciphertext is T: adding M (••xxx) and N (••xx•) produces T (••••x).
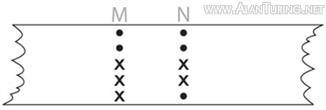
The German engineers selected these rules for dot-and-cross addition so that the following is always true (no matter which letters, or other keyboard characters, are involved): adding one letter (or other character) to another and then adding it again a second time leaves you where you started. In symbols, (x + y) + x = y, for every pair of keyboard characters x and y. For example, adding N to M produces T, as we have just seen, and then adding N to T leads back to M (see right-hand column).
This explains how the receiver’s Tunny decrypted the ciphertext. The ciphertext was produced by adding a stream of key to the plaintext, so by means of adding exactly the same letters of key to the ciphertext, the receiver’s machine wiped away the encryption, exposing the plaintext again.
For example, suppose the plaintext is the single word ‘COLOSSUS’. The stream of key added to the plaintext by the sender’s Tunny might be: WZHI/NR9. These characters are added serially to the letters of ‘COLOSSUS’:
C+W O+Z L+H O+I S+/ S+N U+R S+9.
This produces
XDIVSDFE
(as can be checked by using the table in Appendix 1). ‘XDIVSDFE’ is transmitted over the link. The Tunny at the receiving end adds the same letters of key to the encrypted message:

Tunny. Wheels 1–5 are the psi-wheels, wheels 6 and 7 are the motor-wheels, and wheels 8–12 are the chi-wheels.11

A wheel cam in the operative and inoperative positions.12

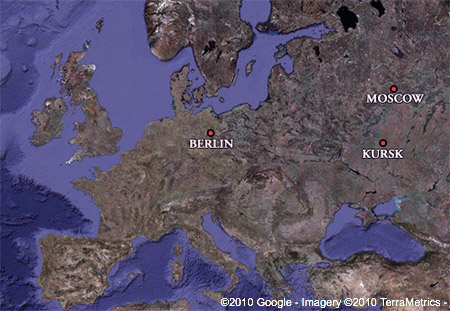
The Battle of Kursk was a turning point of the war.13
X+W D+Z I+H V+I S+/ D+N F+R E+9.
This uncovers the letters
COLOSSUS.
The Tunny machine in fact produces the key-stream by adding together two other letter streams, called at B.P. the psi-stream and the chi-stream (from the Greek letters psi (ψ) and chi (χ)). The psi-stream and the chi-stream are produced by the wheels of the Tunny machine. Let us consider the wheels in more detail.
The twelve wheels form three groups: five psi-wheels, five chi-wheels, and two motor wheels. Each wheel has different numbers of cams (sometimes called ‘pins’) arranged evenly around its circumference (the numbers varying from 23 to 61). The function of the cam is to push a switch as it passes it, so that as the wheel rotates a stream of electrical pulses is generated. The operator can adjust the cams, sliding any that he selects sideways, so that they become inoperative and no longer push the switch when they pass it (see right-hand column). The wheel now causes not a uniform stream of pulses as it turns, but a pattern of pulses and non-pulses—crosses and dots. The arrangement of the cams around the wheel, operative or inoperative, is called the wheel pattern.
Prior to the summer of 1944 the Germans changed the cam patterns of the chi-wheels once every month and the cam patterns of the psi-wheels at first quarterly, then monthly from October 1942. After 1 August 1944, wheel patterns changed daily. The changes were made according to books of wheel patterns issued to Tunny units (different links used different books).
It is the patterns of the cams around the wheels that produces the chi-stream and the psi-stream. Whenever a key is pressed at the keyboard (or a letter read in from the tape in ‘auto’ mode), it causes the five chi-wheels to turn in unison, just far enough for one cam on each wheel to pass its switch. Depending on whether or not that cam is operative, a pulse may or may not be produced. Suppose, for example, that the cam at the first chi-wheel’s switch produces no pulse and the cam on the second likewise produces no pulse at its switch, but the cams on the third and fourth both produce a pulse, and the cam on the fifth produces no pulse. Then the pattern that the chi-wheels produce at this point in their rotation is ••xx•. In other words, the chi-stream at this point contains the letter N. The five psi-wheels also contribute a letter (or other keyboard character) and this is added to N to produce a character of the key-stream.
A complication in the motion of the wheels is that, although the chi-wheels move forward by one cam every time a key is pressed at the keyboard (or a letter arrives from the tape in auto mode, or from the radio receiver), the psi-wheels move irregularly. The psis might all move forward with the chis, or they might all stand still, missing an opportunity to move. This irregular motion of the psi-wheels was described as ‘staggering’ at B.P. Designed to enhance the security of the machine, it turned out to be the crucial weakness.
Whether the psi-wheels move or not is determined by the motor wheels (or in some versions of the machine, by the motor wheels in conjunction with yet other complicating factors). While the psis remain stationary, they continue to contribute the same letter to the key. So the chis might contribute
...KDUGRYMC...
and the psis might contribute
...GGZZZWDD...
Here the chis have moved eight times and the psis only four.
To OKH/OP. ABT. and to OKH/Foreign Armies East, from Army Group South IA/01, No. 411/43, signed von Weichs, General Feldmarschall, dated 25/4:-
Comprehensive appreciation of the enemy for "Zitadelle"
In the main the appreciation of the enemy remains the same as reported in Army Group South (Roman) IIA, No. 0477/43 of 29/3 and in the supplementary appreciation of 15/4. [In Tunny transmissions the word ‘Roman’ was used to indicate a Roman numeral; ‘29/3’ and ‘15/4’ are dates.]
The main concentration, which was already then apparent on the north flank of the Army Group in the general area Kursk--Ssudsha--Volchansk--Ostrogoshsk, can now be clearly recognised: a further intensification of this concentration is to be expected as a result of the continuous heavy transport movements on the lines Yelets--Kastornoye--Kursk, and Povorino--Svoboda and Gryazi--Svoboda, with a probable (B% increase) [‘B%’ indicated an uncertain word] in the area Valuiki--Novy Oskol--Kupyansk. At present however it is not apparent whether the object of this concentration is offensive or defensive. At present, (B% still) in anticipation of a German offensive on both the Kursk and Mius Donetz fronts, the armoured and mobile formations are still evenly distributed in various groups behind the front as strategic reserves.
There are no signs as yet of a merging of these formations or a transfer to the forward area (except for (Roman) II GDS [Guards] Armoured Corps) but this could take place rapidly at any time.
According to information from a sure source the existence of the following groups of the strategic reserve can be presumed:- A) 2 cavalry corps (III GDS and V GDS in the area north of Novocherkassk). It can also be presumed that 1 mech [mechanised] corps (V GDS) is being brought up to strength here. B) 1 mech corps (III GDS) in the area (B% north) of Rowenki. C) 1 armoured corps, 1 cavalry corps and probably 2 mech corps ((Roman) I GD Armoured, IV Cavalry, probably (B% (Roman) I) GDS Mech and V Mech Corps) in the area north of Voroshilovgrad. D) 2 cavalry corps ((B% IV) GDS and VII GDS) in the area west of Starobyelsk. E) 1 mech corps, 1 cavalry corps and 2 armoured corps ((Roman) I GDS (B% Mech), (Roman) I GDS Cavalry, (Roman) II and XXIII Armoured) in the area of Kupyansk--Svatovo. F) 3 armoured corps, 1 mech corps ((Roman) II Armoured, V GDS Armoured, (B% XXIX) Armoured and V GDS Mech under the command of an army (perhaps 5 Armoured Army)) in the area of Ostrogoshsk. G) 2 armoured and 1 cavalry corps ((Roman) II GDS Armoured, III GDS Armoured and VI GDS Cavalry) under the command of an unidentified H.Q., in the area north of Novy Oskol.
In the event of "Zitadelle", there are at present approximately 90 enemy formations west of the line Belgorod--Kursk--Maloarkhangelsk. The attack of the Army Group will encounter stubborn enemy resistance in a deeply echeloned and well developed main defence zone, (with numerous dug in tanks, strong artillery and local reserves) the main effort of the defence being in the key sector Belgorod--Tamarovka.
In addition strong counter attacks by strategic reserves from east and southeast are to be expected. It is impossible to forecast whether the enemy will attempt to withdraw from a threatened encirclement by retiring eastwards, as soon as the key sectors [literally, ‘corner-pillars’] of the bulge in the frontline at Kursk, Belgorod and Maloarkhangelsk, have been broken through. If the enemy throws in all strategic reserves on the Army Group front into the Kursk battle, the following may appear on the battle field:- On day 1 and day 2, 2 armoured divisions and 1 cavalry corps. On day 3, 2 mech and 4 armoured corps. On day 4, 1 armoured and 1 cavalry corps. On day 5, 3 mech corps. On day 6, 3 cavalry corps. On day 6 and/or day 7, 2 cavalry corps.
Summarizing, it can be stated that the balance of evidence still points to a defensive attitude on the part of the enemy: and this is in fact unmistakable in the frontal sectors of the 6 Army and 1 Panzer Army. If the bringing up of further forces in the area before the north wing of the Army Group persists and if a transfer forward and merging of the mobile and armoured formations then takes place, offensive intentions become more probable. In that case it is improbable that the enemy can even then forestall our execution of Zitadelle in the required conditions. Probably on the other hand we must assume complete enemy preparations for defence, including the counter attacks of his strong mot [motorised] and armoured forces, which must be expected.14
The right-hand column contains is a rare survivor—a word-for-word translation of an intercepted Tunny message.15 Dated 25 April 1943 and signed by von Weichs, Commander-in-Chief of German Army Group South, this message was sent from the Russian front to the German Army High Command (‘OKH’—Oberkommando des Heeres). It gives an idea of the nature and quality of the intelligence that Tunny yielded. The enciphered message was intercepted during transmission on the ‘Squid’ radio link between the headquarters of Army Group South and Königsberg.17
The message concerns plans for a major German offensive in the Kursk area codenamed ‘Zitadelle’. Operation Zitadelle was Hitler’s attempt to regain the initiative on the Eastern Front following the Russian victory at Stalingrad in February 1943. Zitadelle would turn out to be one of the crucial battles of the war. Von Weichs’ message gives a detailed appreciation of Russian strengths and weaknesses in the Kursk area. His appreciation reveals a considerable amount about the intentions of the German Army. British analysts deduced from the decrypt that Zitadelle would consist of a pincer attack on the north and south flanks (‘corner-pillars’) of a bulge in the Russian defensive line at Kursk (a line which stretched from the Gulf of Finland in the north to the Black Sea in the south).18 The attacking German forces would then attempt to encircle the Russian troops situated within the bulge.
Highly important messages such as this were conveyed directly to Churchill, usually with a covering note by ‘C’, Chief of the Secret Intelligence Service.19 On 30 April an intelligence report based on the content of the message, but revealing nothing about its origin, was sent to Churchill’s ally, Stalin.20 (Ironically, however, Stalin had a spy inside Bletchley Park: John Cairncross was sending raw Tunny decrypts directly to Moscow by clandestine means.21)
The Germans finally launched operation Zitadelle on 4 July 1943.22 Naturally the German offensive came as no surprise to the Russians—who, with over two months warning of the pincer attack, had amassed formidable defences. The Germans threw practically every panzer division on the Russian front into Zitadelle,23 but to no avail, and on 13 July Hitler called off the attack.24 A few days later Stalin announced in public that Hitler’s plan for a summer offensive against the Soviet Union had been ‘completely frustrated’.25 Zitadelle—the Battle of Kursk—was a decisive turning point on the Eastern front. The counter attack launched by the Russians during Zitadelle developed into an advance which moved steadily westwards, ultimately reaching Berlin in April 1945.
Central figures in the attack on Tunny
Colossus was the brainchild of Thomas H. Flowers (1905–1998). Flowers joined the Telephone Branch of the Post Office in 1926, after an apprenticeship at the Royal Arsenal in Woolwich (well-known for its precision engineering). Flowers entered the Research Branch of the Post Office at Dollis Hill in North London in 1930, achieving rapid promotion and establishing his reputation as a brilliant and innovative engineer. At Dollis Hill Flowers pioneered the use of large-scale electronics, designing equipment containing more than 3000 electronic valves (‘vacuum tubes’ in the US). First summoned to Bletchley Park to assist Turing in the attack on Enigma, Flowers soon became involved in Tunny. After the war Flowers pursued his dream of an all-electronic telephone exchange, and was closely involved with the groundbreaking Highgate Wood exchange in London (the first all-electronic exchange in Europe).




William T. Tutte.19

A British recording of the start of a Tunny message (8 August 1941).The message begins //// //MAR THA99 GUSTA V99LU DWIG9 9OTTO 99BER TA99L UDWIG 99GUS TAV99 OTTO9.20
Max H. A. Newman (1897–1984) was a leading topologist as well as a pioneer of electronic digital computing. A Fellow of St John’s College, Cambridge, from 1923, Newman lectured Turing on mathematical logic in 1935, launching Turing26 on the research that led to the ‘universal Turing machine’, the abstract universal stored-program computer described in Turing’s 1936 paper ‘On Computable Numbers’. At the end of August 1942 Newman left Cambridge for Bletchley Park, joining the Research Section and entering the fight against Tunny. In 1943 Newman became head of a new Tunny-breaking section known simply as the Newmanry, home first to the experimental ‘Heath Robinson’ machine and subsequently to Colossus. By April 1945 there were ten Colossi working round the clock in the Newmanry. The war over, Newman took up the Fielden Chair of Mathematics at the University of Manchester and—inspired both by Colossus and by Turing’s abstract ‘universal machine’—lost no time in establishing a facility to build an electronic stored-program computer. On 21 June 1948, in Newman’s Computing Machine Laboratory, the world’s first electronic stored-program digital computer, the Manchester ‘Baby’, ran its first program.
John Tiltman (1894–1982) was seconded to the Government Code and Cypher School (GC & CS) from the British army in 1920, in order to assist with Russian diplomatic traffic.27 An instant success as a codebreaker, Tiltman never returned to ordinary army duties. From 1933 onwards he made a series of major breakthroughs against Japanese military ciphers, and in the early years of the war he also broke a number of German ciphers, including the army’s double Playfair system, and the version of Enigma used by the German railway authorities. In 1941 Tiltman made the first significant break into Tunny. Promoted to Brigadier in 1944, he went on to become a leading member of GCHQ, GC & CS’s peacetime successor. Following his retirement from GCHQ in 1964, Tiltman joined the National Security Agency, where he worked until 1980.
Alan M. Turing (1912–1954) was elected a Fellow of King’s College, Cambridge in 1935, at the age of only 22. ‘On Computable Numbers’, published the following year, was his most important theoretical work. It is often said that all modern computers are Turing machines in hardware: in a single article, Turing ushered in both the modern computer and the mathematical study of the uncomputable. During the early stages of the war, Turing broke German Naval Enigma and produced the logical design of the ‘Bombe’, an electro-mechanical code-breaking machine. Hundreds of Bombes formed the basis of Bletchley Park’s factory-style attack on Enigma. Turing briefly joined the attack on Tunny in 1942, contributing a fundamentally important cryptanalytical method known simply as ‘Turingery’. In 1945, inspired by his knowledge of Colossus, Turing designed an electronic stored-program digital computer, the Automatic Computing Engine (ACE). At Bletchley Park, and subsequently, Turing pioneered Artificial Intelligence: while the rest of the post-war world was just waking up to the idea that electronics was the new way to do binary arithmetic, Turing was talking very seriously about programming digital computers to think. He also pioneered the discipline now known as Artificial Life, using the Ferranti Mark I computer at Manchester University to model biological growth.28
William T. Tutte (1917–2002) specialised in chemistry in his undergraduate work at Trinity College, Cambridge, but was soon attracted to mathematics. He was recruited to Bletchley Park early in 1941, joining the Research Section. Tutte worked first on the Hagelin cipher machine and in October 1941 was introduced to Tunny. Tutte’s work on Tunny, which included deducing the structure of the Tunny machine, can be likened in importance to Turing’s earlier work on Enigma. At the end of the war, Tutte was elected to a Research Fellowship in mathematics at Trinity; he went on to found the area of mathematics now called graph theory.
From time to time German operators used the same wheel settings for two different messages, a circumstance called a depth. It was thanks to the interception of depths, in the summer of 1941, that the Research Section at B.P. first found its way into Tunny.
Prior to October 1942, when QEP books were introduced, the sending operator informed the receiver of the starting positions of the 12 wheels by transmitting an unenciphered group of 12 letters. The first letter of the 12 gave the starting position of the first psi-wheel, and so on for the rest of the wheels. For example, if the first letter was ‘M’ then the receiver would know from the standing instructions for the month to set his first psi-wheel to position 31, say. At B.P. this group of letters was referred to as the message’s indicator. Sometimes the sending operator would expand the 12 letters of the indicator into 12 unenciphered names: Martha Gustav Ludwig Otto... instead of MGLO..., for example (see right-hand column). The occurrence of two messages with the same indicator was the tell-tale sign of a depth.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| J | S | H | 5 | N | Z | Y | M | F | S | 0 | 1 | 1 | 5 | I | V | K | U | 1 | Y | U | 4 | N | C | E | J | E | G | P | B |
| J | S | H | 5 | N | Z | Y | Z | Y | 5 | G | L | F | R | G | X | O | 5 | S | Q | 5 | D | A | 1 | J | J | H | D | 5 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | f | o | u | g | f | 1 | 4 | m | a | q | s | g | 5 | s | e | k | z | r | 0 | y | w | h | e |
| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 |
| M | N | T | Q | M | A | 0 | U | 4 | Y | L | 1 | Q | I | J | L | Y | V | I | N | U | B | 2 | 3 | R | 5 | W | E | V | G |
| B | K | S | U | C | B | T | T | O | 5 | E | 4 | T | S | L | E | 3 | F | G | Z | Y | U | H | V | H | 3 | H | E | E | 0 |
| s | a | y | t | l | g | t | q | t | q | w | q | u | a | b | w | c | w | m | x | l | v | t | s | v | b | u | 0 | 1 | g |
| 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 |
| Q | I | 2 | 4 | 5 | G | R | J | M | L | C | Y | 5 | 0 | H | K | A | S | 1 | I | S | 5 | X | U | N | S | R | Z | Z | B |
| T | G | 2 | H | H | 1 | Q | J | X | V | K | 1 | B | J | M | K | 2 | O | M | Z | Y | V | I | N | 3 | H | M | C | 3 | D |
| u | m | 0 | m | p | s | x | 0 | e | n | e | r | 3 | j | 4 | 0 | u | x | a | q | t | m | 3 | j | q | z | p | 1 | r | t |
| 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 |
| D | B | B | 1 | C | L | S | Q | H | H | U | H | 5 | X | D | 0 | F | N | 3 | J | 3 | V | O | C | A | D | J | C | D | N |
| U | Q | 3 | 4 | Z | R | 2 | M | R | M | O | H | 5 | J | Q | P | W | U | E | Y | C | P | R | G | 1 | L | D | A | T | I |
| c | c | 5 | q | 1 | o | e | j | v | 4 | 1 | 0 | 0 | p | v | p | v | j | g | v | y | 4 | 1 | h | m | 3 | 5 | f | b | r |
So when on 30 August 1941 two messages with the same indicator were intercepted, B.P. suspected that they had found a depth. As it turned out, the first transmission had been corrupted by atmospheric noise, and the message was resent at the request of the receiving operator. Had the sender repeated the message identically, the use of the same wheel settings would have left B.P. none the wiser. However, in the course of the second transmission the sender introduced abbreviations and other minor deviations (the message was approximately 4000 characters long). So the depth consisted of two not-quite-identical plaintexts each encrypted by means of exactly the same sequence of key—a codebreaker’s dream.
On the hypothesis that the machine had produced the ciphertext by
adding a stream of key to the plaintext, Tiltman added the two
ciphertexts (see right-hand column). If the hypothesis were correct, this would have the
effect of cancelling out the key (since, as previously mentioned,


Alan Turing. ‘We might have lost the war without him.’23

Tiltman managed to prise the two individual plaintexts out of this string (it took him ten days). He had to guess at words of each message, and Tiltman was a very good guesser. Each time he guessed a word from one message, he added it to the characters at the right place in the string, and if the guess was correct an intelligible fragment of the second message would pop out. For example, adding the probable word ‘geheim’ (secret) to characters 83-88 of the string reveals the plausible fragment ‘eratta’.29 This short break can then be extended to the left and right. More letters of the second message are obtained by guessing that ‘eratta’ is part of ‘militaerattache’ (military attache), and if these letters are added to their counterparts in the string, further letters of the first message are revealed. And so on. Eventually Tiltman achieved enough of these local breaks to realise that long stretches of each message were the same, and so was able to decrypt the whole thing.
Adding the plaintext deduced by Tiltman to its corresponding ciphertext revealed the sequence of key used to encrypt the messages. These 4000 characters of key were passed to Tutte and, in January 1942, Tutte single-handedly deduced the fundamental structure of the Tunny machine. He focussed on just one of the five ‘slices’ of the key-stream, the top-most row were the key-stream to be punched on tape. Each of these five slices was called an ‘impulse’ at B.P. (In the ‘Colossus’ punched tape shown earlier, the first impulse is ••••xxxx, the second is x•x•••x•, and so on.)
The top-most impulse of the key-stream, Tutte managed to deduce, was the result of adding two streams of dots and crosses. The two streams were produced by a pair of wheels, which he called ‘chi’ and ‘psi’. The chi-wheel, he determined, always moved forward one place from one letter of text to the next, and the psi-wheel sometimes moved forwards and sometimes stayed still. It was a remarkable feat of cryptanalysis. At this stage the rest of the Research Section joined in and soon the whole machine was laid bare, without any of them ever having set eyes on one.
Now that Bletchley knew the nature of the machine, the next step was to devise methods for breaking the daily traffic. A message could be read if the wheel settings and the wheel patterns were known. The German operators themselves were revealing each message’s setting via the 12-letter indicator. Thanks to Tutte’s feat of reverse-engineering, the wheel patterns were known for August 1941. The codebreaker’s problem was to keep on top of the German’s regular changes of wheel-pattern.
In
July 1942 Turing invented a method for finding wheel-patterns from
depths—‘Turingery’. Turing was at that time on loan
to the Research Section from Hut 8 and the struggle against Naval
Enigma.30 Turingery was the third of the three
strokes of genius that Turing contributed to the attack on the German
codes, along with his design for the Bombe and his unravelling of the
form of Enigma used by the Atlantic U-boats.31 As
fellow codebreaker Jack Good observed, ‘I won’t say that
what Turing did made us win the war, but I daresay we might have lost
it without him’.32
Turingery was a hand method, involving paper, pencil and eraser. Beginning with a stretch of key obtained from a depth, Turingery enabled the breaker to prize out from the key the contribution that the chi-wheels had made. The cam-patterns of the individual chi-wheels could be inferred from this. Further deductions led to the cam-patterns of the psi- and motor-wheels. Once gained via Turingery, this information remained current over the course of many messages. Eventually the patterns were changed too frequently for any hand method to be able to cope (there were daily changes of all patterns from August 1944), but by that time Colossus, not Turingery, was being used for breaking the wheel patterns.
|
M |
N |
T |
M + N |
N + T |
|
• |
• |
• |
• |
• |
|
• |
• |
• |
• |
• |
|
x |
x |
• |
• |
x |
|
x |
x |
• |
• |
x |
|
x |
• |
x |
x |
x |
Basic to Turingery was the idea of forming the delta of a stream of characters. (Delta-ing a character-stream was also called ‘differencing’ the stream.) The delta of a character-stream is the stream that results from adding together each pair of adjacent letters in the original stream. For example, the delta of the short stream MNT (sometimes written ΔMNT) is produced by adding M to N and N to T (using the rules of dot-and-cross addition explained previously). The delta of MNT is in fact TM, as the table in the right-hand column shows (the shaded columns contain the delta).



The idea of the delta is that it tracks changes in the original stream. If a dot follows a dot or a cross follows a cross at a particular point in the original stream, then the corresponding point in the delta has a dot (see the table). A dot in the delta means ‘no change’. When, on the other hand, there is a cross followed by a dot or a dot followed by a cross in the original stream, then the corresponding point in the delta has a cross. A cross in the delta means ‘change’. Turing introduced the concept of delta in July 1942, observing that by delta-ing a stretch of key he was able to make deductions which could not be made from the key in its un-deltaed form.33
Turingery worked on deltaed key to produce the deltaed contribution of the chi-wheels. Turing’s discovery that delta-ing would reveal information otherwise hidden was essential to the developments that followed. The algorithms implemented in Colossus (and in its precursor Heath Robinson) depended on this simple but brilliant observation. In that sense, the entire machine-based attack on Tunny flowed from this fundamental insight of Turing’s.
How did Turingery work? The method exploited the fact that each impulse of the chi-stream (and also its delta-ed form) consists of a pattern that repeats after a fixed number of steps. Since the number of cams on the 1st chi-wheel is 41, the pattern in the first impulse of the chi-stream repeats every 41 steps. In the 2nd impulse the pattern repeats every 31 steps—the number of cams on the 2nd chi-wheel—and for the 3rd, 4th and 5th impulses, the wheels have 29, 26, and 23 cams respectively. Therefore a hypothesis about the identity, dot or cross, of a particular bit in, say, the first impulse of the chi will, if correct, also produce the correct bit 41 steps further on, and another 41 steps beyond that, and so on. Given 500 letters of key, a hypothesis about the identity of a single letter of the chi (or delta-ed chi) will yield approximately 500/41 bits of the first impulse, 500/31 bits of the second impulse, 500/29 bits of the third, and so on—a total of about 85 bits.
In outline, Turing’s method is this. The first step is to make a guess: the breaker guesses a point in the delta-ed key at which the psi-wheels stayed still in the course of their ‘staggering’ motion. Whatever guess is made, it has a 50% chance of being right. Positions where the psis did not move are of great interest to the breaker, since at these positions the deltaed key and the deltaed chi are identical. (The reason for this is that the deltaed contribution of the psis at such positions is •••••, and adding ••••• to a letter does not alter the letter.) Because the key is known, the letter of the deltaed chi at the guessed position is also known—assuming, of course, that the guess about the psis not having moved is correct. Given this single letter of the deltaed chi, a number of bits can then be filled in throughout the five impulses, by propagating to the left and right at the appropriate periods.
Now that various bits of the delta chi are filled in, guesses can be made as to the identity of others letters. For example, if one letter of the delta chi is •???• and the corresponding letter of the delta key is •xxx• (C), the breaker may guess that this is another point at which the psis stood still, and replace •???• in the delta chi by •xxx•. This gives three new bits to propagate left and right. And so the process continues, with more and more bits of the delta chi being written in.
Naturally the breaker’s guesses are not always correct, and as the process of filling in bits goes on, any incorrect guesses will tend to produce clashes—places where both a cross and a dot are assigned to the same position in the impulse. Guesses that are swamped by clashes have to be revised. With patience, luck, a lot of rubbing out, and a lot of cycling back and forth between putative fragments of delta chi and delta psi, a correct and complete stretch of delta chi eventually emerges.


Newman.28


Machines in the Newmanry at Bletchley Park for processing punched tape.30

The intercept station at Flowerdown.31

Jerry Roberts, leading codebreaker in the Testery.32
Tunny
could now be tackled operationally, and a Tunny-breaking section was
immediately set up under Major Ralph Tester.34
Several members of the Research Section moved over to the ‘Testery’.
Armed with Turingery and other hand methods, the Testery read nearly
every message from July to October 1942—thanks
to the insecure 12-letter indicator system, by means of which the
German operator obligingly conveyed the wheel setting to the
codebreakers.35 In October, however, the indicators were replaced by
numbers from the QEP books, and the Testery, now completely reliant
on depths, fell on leaner times. With the tightening up of German
security, depths were becoming increasingly scarce. The Research
Section renewed its efforts against Tunny, looking for a means of
finding wheel settings that did not depend on depths.36
In November 1942 Tutte invented a way of discovering the settings of messages not in depth. This became known as the ‘Statistical Method’. The rub was that at first Tutte’s method seemed impractical. It involved calculations which, if done by hand, would consume a vast amount of time—probably as much as several hundred years for a single, long message, Newman once estimated.37
The necessary calculations were straightforward enough, consisting basically of comparing two streams made up of dots and crosses, and counting the number of times that each had a dot, or cross, in the same position. Today, of course, we turn such work over to electronic computers. When Tutte shyly explained his method to Newman, Newman suggested using high-speed electronic counters to mechanise the process. It was a brilliant idea. Within a surprisingly short time a factory of monstrous electronic computers dedicated to breaking Tunny was affording a glimpse of the future.
Electronic counters had been developed in Cambridge before the war. Used for counting emissions of sub-atomic particles, these had been designed by C. E. Wynn-Williams, a Cambridge don.38 Newman knew of Wynn-Williams’ work, and in a moment of inspiration he saw that the same idea could be applied to the Tunny problem. Within a month of Tutte’s inventing his statistical method Newman began developing the necessary machine. He worked out the cryptanalytical requirements for the machine and called in Wynn-Williams to design the electronic counters. Construction of Newman’s machine started in January 1943 and a prototype began operating in June of that year, in the newly formed Tunny-breaking section called the ‘Newmanry’. The prototype machine was soon dubbed ‘Heath Robinson’, after the famous cartoonist who drew overly-ingenious mechanical contrivances.
Tutte’s method delivered the settings of the chi wheels. Once the Newmanry had discovered the settings of the chis by machine, the contribution that the chis had made to the ciphertext was stripped away, producing what was called the ‘de-chi’ of the message. The de-chi was made by a replica of the Tunny machine, designed by Flowers’ Post Office engineers at Dollis Hill. The de-chi was then passed to the Testery, where a cryptanalyst would break into it by ‘ordinary’ pencil-and-paper methods requiring only (as a wartime document described it) ‘the power of instantaneous mental addition of letters of the Teleprint alphabet’.39
The reason it was feasible to break the de-chi by hand was that the staggering motion of the psi-wheels introduced local regularities. Once the contribution of the chis had been stripped out of the key, what remained of the key contained distinctive patterns of repeated letters, e.g. ...GGZZZWDD..., since while the psis stood still they continued to contribute the same letter. By latching onto these repetitions, the cryptanalyst could uncover some stretches of this residual key, and this in turn enabled the settings of the psi-wheels and the motor-wheels to be deduced. For example, adding the guessed word ‘dringend’ (‘urgent’) to the de-chi near the beginning of the message might produce 888EE00WW—pure gold, confirming the guess. With luck, once a break was achieved it could be extended to the left or right, in this case perhaps by trying on the left ‘sehr9’ (‘very’ followed by a space), and on the right ++M88, the code for a full stop (see Appendix 1). Once the codebreaker had a short stretch of the key that the psi-wheels had contributed, the wheel settings could usually be obtained by comparing the key to the known wheel patterns. When all the wheel-settings were known, the ciphertext was keyed into one of the Testery’s replica Tunny machines, and the German plaintext would emerge.
In order to illustrate the basic ideas of Tutte’s method for finding the settings of the chi wheels, let us assume that we have an intercepted ciphertext 10,000 characters long. This ciphertext is punched on a tape (we call this the ‘message-tape’). An assistant, who knows the chi-wheel patterns, provides us with a second tape (the ‘chi-tape’). This assistant has worked out the machine’s entire chi-stream, beginning at an arbitrarily selected point in the revolution of the chi-wheels, and stepping through all their possible joint combinations. (Once the wheels have moved through all the possible combinations, their capacity for novelty is exhausted, and should the wheels continue to turn they merely duplicate what has gone before.) The complete chi-stream is, of course, rather long, but eventually the assistant does produce a roll of tape with the stream punched on it. The sequence of 10,000 consecutive characters of chi-stream that was used to encrypt our message is on this tape somewhere—our problem is to find it. This sequence is called simply ‘the chi’ of the message. Tutte’s method exploits a fatal weakness in the design of the Tunny machine, a weakness again stemming from the staggering motion of the psi-wheels. The central idea of the method is this: The chi is recognisable on the basis of the ciphertext, provided the wheel patterns are known. Tutte showed by a clever mathematical deduction that the delta of the ciphertext and the delta of the chi would usually correspond slightly. That slightly is the key to the whole business—any degree of regularity, no matter how weak, is the cryptanalyst’s friend. The slight regularity that Tutte discovered could be used as a touchstone for finding the chi. (Readers interested in Tutte’s mathematical reasoning will find the details in Appendix 2: The Tunny encipherment equation and Tutte’s 1 + 2 break-in. At present we will concentrate on how the method is carried out.)
We select the first 10,000 characters of the chi-tape; we will compare this stretch of the chi-tape with the message-tape. Tutte showed that in fact we need examine only the first and the second of the five horizontal rows punched along the chi-tape, the first and second impulses (these two rows are the contributions of the first and second chi-wheels respectively). Accordingly we need consider only the first and second impulses of the message-tape. This simplifies considerably the task of comparing the two tapes. Because Tutte’s method focussed on the first and second chi-wheels it was dubbed the ‘1+2 break in’.40
Here is the procedure for comparing the message-tape with the stretch of chi-tape we have picked. First, we add the first and second impulses of the message-tape and form the delta of the resulting sequence of dots and crosses. (For example, if the sequence produced by adding the two impulses begins x•x..., the delta begins xx... .) Second, we add the first and second impulses of the 10,000-character piece of chi-tape, and again form the delta of the result. Next we lay these two deltas side by side and count how many times they have dots in the same places and how many times crosses. We add the two tallies to produce a total score for this particular piece of the chi-tape. We are looking for a match between the two deltas of around 55%. Tutte showed that this is the order of correspondence that can be expected when the piece of chi-tape under examination contains the first and second impulses of the actual chi.
The first score we obtain probably won’t be anything special—for we would be extremely lucky if the first 10,000 characters of chi-stream that we examined were the chi of the message. So next we shift along one character in the chi-stream and focus on a new candidate for the message’s chi, the 2nd through to the 10,001st characters on the chi-tape (see the diagram in the right-hand column). We add, delta, and count once again. Then we shift along another character, repeating the process until we have examined all candidates for the chi. A buoyant score reveals the first and second impulses of the actual chi (we hope).
Once a winning segment of the chi-tape has been located, its place within the complete chi-stream tells us the positions of the first and second chi-wheels at the start of the message. With these settings in hand, a similar procedure is used to chase the settings of the other chi-wheels.
As mentioned previously, the cause of the slight regularity that Tutte latched onto is at bottom the staggering movement of the psi-wheels—the great weakness of the Tunny machine. While the psis remained stationary, they continued to contribute the same letter to the key; and so, since delta-ing tracks change, the delta of the stream of characters contributed by the psis contained more dots than crosses (recall that a cross in the delta indicates a change). Tutte calculated that there would usually be about 70% dot in the delta of the sum of the contributions of the first two psi-wheels.
The delta of the plaintext also contained more dots than crosses (for reasons explained in Appendix 2, which included the fact that Tunny operators habitually repeated certain characters). Tutte investigated a number of broken messages and discovered to his delight that the delta of the sum of the first two impulses was as a rule about 60% dot. Since these statistical regularities in the delta of the psi and the delta of the plain both involved a predominance of dot over cross, they tended to reinforce one another. Tutte deduced that their net effect, in favourable cases, would be the agreement, noted above, of about 55% between the processed ciphertext and the processed chi.


The Telecommunications Research Establishment (TRE) in Malvern.36

Flowers lecturing at the National Physical Laboratory in 1977.37
A relay.38




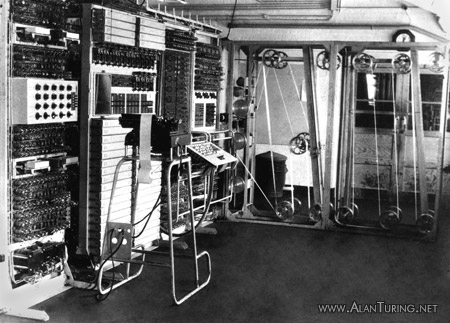

Side view of Colossus VII. The four large boxes on the rear frame are the power supply units.44
Colossus, from a sketch by Flowers.45




Some of the controls on Colossus VI.49

Donald Michie.50

W. W. Chandler.51
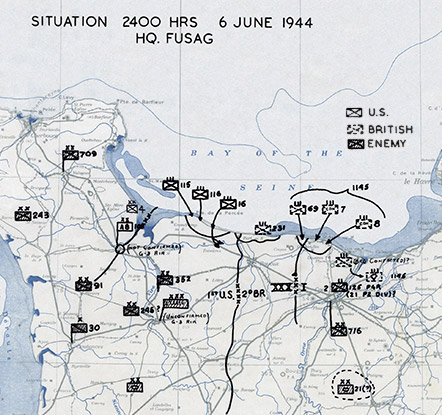
The D-day landing sites on the beaches of Normandy.52

Approaching Omaha beach on D-day.53

The D-day landings.54

Sturgeon.55
Tunny’s security depended on the appearance of randomness, and here was a crack in the appearance. The British seized on it. If, instead of the psi-wheels either all moving together or all standing still, the designers had arranged for them to move independently—or even to move regularly like the chis—then the chink that let Tutte in would not have existed.
Smoke rose from Newman’s prototype machine the first time it was switched on (a large resistor overloaded). Around a vast frame made of angle-iron wound two long loops of teleprinter tape (see photo). Resembling an old-fashioned bed standing on end, the frame quickly became known as the ‘bedstead’. The tapes were supported by a system of pulleys and wooden wheels of diameter about ten inches. Each tape was driven by a toothed sprocket-wheel which engaged a continuous row of sprocket-holes along the centre of the tape (see previous diagram). The tapes were driven by the same drive-shaft and moved in synchronisation with each other at a maximum speed of 2000 characters per second. To the amusement and annoyance of Heath Robinson’s operators, tapes would sometimes tear or come unglued, flying off the bedstead at high speed and breaking into fragments which festooned the Newmanry.
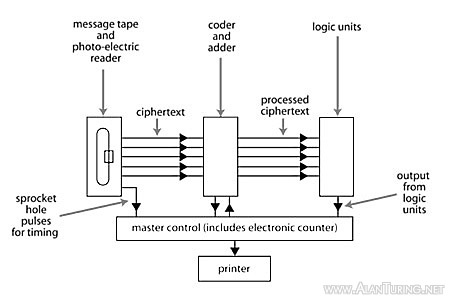
One tape was the message-tape and the other the chi-tape. In practice the chi-tape might contain, for example, only the first and second impulses of the complete chi-stream, resulting in a shorter tape. The drive mechanism was arranged so that as the tapes ran on the bedstead, the message-tape stepped through the chi-tape one character at a time (see previous diagram). Photo-electric readers mounted on the bedstead converted the hole/no-hole patterns punched on the tapes into streams of electrical pulses, and these were routed to a ‘combining unit’—a logic unit, in modern terminology. The combining unit did the adding and the delta-ing, and Wynn-Williams’ electronic counters produced the scores. The way the combining was done could be varied by means of replugging cables, a primitive form of programming. The combining unit, the bedstead and the photo-electric readers were made by Post Office engineers at Dollis Hill and the counters by Wynn-Williams’ unit at the Telecommunications Research Establishment (TRE).41
Heath Robinson worked, proving in a single stroke that Newman’s idea of attacking Tunny by machine was worth its salt and that Tutte’s method succeeded in practice. However, Heath Robinson suffered from ‘intolerable handicaps’.42 Despite the high speed of the electronic counters, Heath Robinson was not really fast enough for the codebreakers’ requirements, taking several hours to elucidate a single message.43 Moreover, the counters were not fully reliable—Heath Robinson was prone to deliver different results if set the same problem twice. Mistakes made in hand-punching the two tapes were another fertile source of error, the long chi-tape being especially difficult to prepare. At first, undetected tape errors prevented Heath Robinson from obtaining any results at all.44 And paramount among the difficulties was that the two tapes would get out of synchronisation with each other as they span, throwing the calculations out completely. The loss of synchronisation was caused by the tapes stretching, and also by uneven wear around the sprocket holes.
The question was how to build a better machine—a question for an engineer. In a stroke of genius, the electronics expert Thomas Flowers solved all these problems.
Flowers, neglected pioneer of computing
During the 1930s Flowers pioneered the large-scale use of electronic valves to control the making and breaking of telephone connections.45 He was swimming against the current. Many regarded the idea of large-scale electronic equipment with scepticism. The common wisdom was that valves—which, like light bulbs, contained a hot glowing filament—could never be used satisfactorily in large numbers, for they were unreliable, and in a large installation too many would fail in too short a time. However, this opinion was based on experience with equipment that was switched on and off frequently—radio receivers, radar, and the like. What Flowers discovered was that, so long as valves were switched on and left on, they could operate reliably for very long periods, especially if their ‘heaters’ were run on a reduced current.
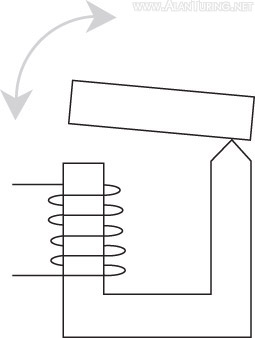
At that time, telephone switchboard equipment was based on the relay. A relay is a small, automatic switch. It contains a mechanical contact-breaker—a moving metal rod that opens and closes an electrical circuit. The rod is moved from the ‘off’ position to the ‘on’ position by a magnetic field. A current in a coil is used to produce the magnetic field; as soon as the current flows, the field moves the rod. When the current ceases, a spring pushes the rod back to the ‘off’ position. Flowers recognised that equipment based instead on the electronic valve—whose only moving part is a beam of electrons—not only had the potential to operate very much faster than relay-based equipment, but was in fact potentially more reliable, since valves are not prone to mechanical wear.
In 1934 Flowers wired together an experimental installation containing three to four thousand valves (by contrast, Wynn-Williams’ electronic counters of 1931 contained only three or four valves). This equipment was for controlling connections between telephone exchanges by means of tones, like today’s touch-tones (a thousand telephone lines were controlled, each line having 3-4 valves attached to its end). Flowers’ design was accepted by the Post Office and the equipment went into limited operation in 1939. Flowers had proved that an installation containing thousands of valves would operate very reliably—but this equipment was a far cry from Colossus. The handful of valves attached to each telephone line formed a simple unit, operating independently of the other valves in the installation, whereas in Colossus large numbers of valves worked in concert.
During the same period before the war Flowers explored the idea of using valves as high-speed switches. Valves were used originally for purposes such as amplifying radio signals. The output would vary continuously in proportion to a continuously varying input, for example a signal representing speech. Digital computation imposes different requirements. What is needed for the purpose of representing the two binary digits, 1 and 0, is not a continuously varying signal but plain ‘on’ and ‘off’ (or ‘high’ and ‘low’). It was the novel idea of using the valve as a very fast switch, producing pulses of current (pulse for 1, no pulse for 0) that was the route to high-speed digital computation. During 1938-9 Flowers worked on an experimental high-speed electronic data store embodying this idea. The store was intended to replace relay-based data stores in telephone exchanges. Flowers’ long-term goal was that electronic equipment should replace all the relay-based systems in telephone exchanges.
By the time of the outbreak of war with Germany, only a small number of electrical engineers were familiar with the use of valves as high-speed digital switches. Thanks to his pre-war research, Flowers was (as he himself remarked) possibly the only person in Britain who realized that valves could be used reliably on a large scale for high-speed digital computing.46 When Flowers was summoned to Bletchley Park—ironically, because of his knowledge of relays—he turned out to be the right man in the right place at the right time.
Turing, working on Enigma, had approached Dollis Hill to build a relay-based decoding machine to operate in conjunction with the Bombe (the Bombe itself was also relay-based). Once the Bombe had uncovered the Enigma settings used to encrypt a particular message, these settings were to be transferred to the machine requisitioned by Turing, which would automatically decipher the message and print out the German plaintext.47 Dollis Hill sent Flowers to Bletchley Park. He would soon become one of the great figures of World War II codebreaking. In the end, the machine Flowers built for Turing was not used, but Turing was impressed with Flowers, who began thinking about an electronic Bombe, although he did not get far. When the teleprinter group at Dollis Hill ran into difficulties with the design of the Heath Robinson’s combining unit, Turing suggested that Flowers be called in. (Flowers was head of the switching group at Dollis Hill, located in the same building as the teleprinter group.) Flowers and his switching group improved the design of the combining unit and manufactured it.48
Flowers did not think much of the Robinson, however. The basic design had been settled before he was called in and he was sceptical as soon as Morrell, head of the teleprinter group, first told him about it. The difficulty of keeping two paper tapes in synchronisation at high speed was a conspicuous weakness. So was the use of a mixture of valves and relays in the counters, because the relays slowed everything down: Heath Robinson was built mainly from relays and contained no more than a couple of dozen valves. Flowers doubted that the Robinson would work properly and in February 1943 he presented Newman with the alternative of a fully electronic machine able to generate the chi-stream (and psi- and motor-streams) internally.49
Flowers’ suggestion was received with ‘incredulity’ at TRE and Bletchley Park.50 It was thought that a machine containing the number of valves that Flowers was proposing (between one and two thousand) ‘would be too unreliable to do useful work’.51 In any case, there was the question of how long the development process would take—it was felt that the war might be over before Flowers’ machine was finished. Newman pressed ahead with the two-tape machine. He offered Flowers some encouragement but effectively left him to do as he wished with his proposal for an all-electronic machine. Once Heath Robinson was a going concern, Newman placed an order with the Post Office for a dozen more relay-based two-tape machines (it being clear, given the quantity and very high importance of Tunny traffic, that one or two machines would not be anywhere near enough). Meanwhile Flowers, on his own initiative and working independently at Dollis Hill, began building the fully electronic machine that he could see was necessary. He embarked on Colossus, he said, ‘in the face of scepticism’52 from Bletchley Park and ‘without the concurrence of BP’.53 ‘BP weren’t interested until they saw it [Colossus] working’, he recollected.54 Fortunately, the Director of the Dollis Hill Research Station, Gordon Radley, had greater faith in Flowers and his ideas, and placed ‘the whole resources of the laboratories’ at Flowers’ disposal.55
The prototype Colossus was brought to Bletchley Park in lorries and reassembled by Flowers’ engineers.56 It had approximately 1600 electronic valves and operated at 5000 characters per second. Later models, containing approximately 2400 valves, processed five streams of dot-and-cross simultaneously, in parallel. This boosted the speed to 25,000 characters per second. Colossus generated the chi-stream electronically. Only one tape was required, containing the ciphertext—the synchronisation problem vanished. (Flowers’ original plan was to dispense with the message tape as well and set up the ciphertext, as well as the wheels, on valves; but he abandoned this idea when it became clear that messages of 5000 or more characters would have to be processed.57)
The arrival of the prototype Colossus caused quite a stir. Flowers said:
I don’t think they [Newman et al.] really understood what I was saying in detail — I am sure they didn’t — because when the first machine was constructed and working, they obviously were taken aback. They just couldn’t believe it! ... I don’t think they understood very clearly what I was proposing until they actually had the machine.58
On what date did Colossus first come alive? In his written and verbal recollections Flowers was always definite that Colossus was working at Bletchley Park in the early part of December 1943.59 In three separate interviews he recalled a key date quite specifically, saying that Colossus carried out its first trial run at Bletchley Park on 8 December 1943.60 However, Flowers’ personal diary for 1944—not discovered until after his death—in fact records that Colossus did not make the journey from Dollis Hill to Bletchley Park until January 1944. On Sunday 16 January Colossus was still in Flowers’ lab at Dollis Hill. His diary entry shows that Colossus was certainly working on that day. Flowers was busy with the machine from the morning until late in the evening and he slept at the lab.
Flowers’ entry for 18 January reads simply: ‘Colossus delivered to B.P.’. This is confirmed by a memo dated 18 January from Newman to Travis (declassified only in 2004). Newman wrote ‘Colossus arrives to-day’.61 Colossus cannot therefore have carried out its first trial run at Bletchley Park in early December. What did happen on 8 December 1943, the date that stuck so firmly in Flowers’ mind? Perhaps this was indeed the day that Colossus processed its first test tape at Dollis Hill. ‘I seem to recall it was in December’, says Harry Fensom, one of Flowers’ engineers.62
By February 1944 the engineers had got Colossus ready to begin serious work for the Newmanry. Tutte’s statistical method could now be used at electronic speed. The computer attacked its first message on Saturday 5 February. Flowers was present. He noted laconically in his diary, ‘Colossus did its first job. Car broke down on way home.’
Colossus immediately doubled the codebreakers’ output.63 The advantages of Colossus over Robinson were not only its greatly superior speed and the absence of synchronised tapes, but also its greater reliability, resulting from Flowers’ redesigned counters and the use of valves in place of relays throughout. It was clear to the Bletchley Park authorities—whose scepticism was now completely cured—that more Colossi were required urgently.
Indeed, a crisis had developed, making the work of Newman’s section even more important than before. Since the German introduction of the QEP system in October 1942, the codebreakers using hand-methods to crack Tunny messages had been reliant upon depths, and as depths became rarer during 1943, the number of broken messages reduced to a trickle.64 Then things went from bad to worse. In December 1943 the Germans started to make widespread use of an additional device in the Tunny machine, whose effect was to make depth-reading impossible (by allowing letters of the plaintext itself to play a role in the generation of the key). The hand breakers had been prone to scoff at the weird contraptions in the Newmanry, but suddenly Newman’s machines were essential to all Tunny work.65
In March 1944 the authorities demanded four more Colossi. By April they were demanding twelve.66 Great pressure was put on Flowers to deliver the new machines quickly. The instructions he received came ‘from the highest level’—the War Cabinet—and he caused consternation when he said flatly that it was impossible to produce more than one new machine by 1 June 1944.67
Flowers had managed to produce the prototype Colossus at Dollis Hill only because many of his laboratory staff ‘did nothing but work, eat, and sleep for weeks and months on end’.68 He needed greater production capacity, and proposed to take over a Post Office factory in Birmingham. Final assembly and testing of the computers would be done at his Dollis Hill laboratory. Flowers estimated that once the factory was in operation he would be able to produce additional Colossi at the rate of about one per month.69 He recalled how one day some Bletchley people came to inspect the work, thinking that Flowers might be ‘dilly-dallying’: they returned ‘staggered at the scale of the effort’.70 Churchill for his part gave Flowers top priority for everything he needed.71
By means of repluggable cables and panels of switches, Flowers deliberately built more flexibility than was strictly necessary into the logic units of the prototype Colossus. As a result, new methods could be implemented on Colossus as they were discovered. In February 1944 two members of the Newmanry, Donald Michie and Jack Good, had quickly found a way of using Colossus to discover the Tunny wheel patterns.72 Flowers was told to incorporate a special panel for breaking wheel patterns in Colossus II.
Colossus II—the first of what Flowers referred to as the ‘Mark 2’ Colossi73—was shipped from Dollis Hill to Bletchley Park on 4 May 1944.74 The plan was to assemble and test Colossus II at Bletchley Park rather than Dollis Hill, so saving some precious time.75 Promised by the first of June, Colossus II was still not working properly as the final hours of May ticked past. The computer was plagued by intermittent and mysterious faults.76 Flowers struggled to find the problem, but midnight came and went. Exhausted, Flowers and his team dispersed at 1 am to snatch a few hours sleep.77 They left Chandler to work on, since the problem appeared to be in a part of the computer that he had designed. It was a tough night: around 3 am Chandler noticed that his feet were getting wet.78 A radiator pipe along the wall had sprung a leak, sending a dangerous pool of water towards Colossus.
Flowers returned to find the computer running perfectly. ‘Colossus 2 in operation’, he noted in his diary.79 The puddle remained, however, and the women operators had to don gumboots to insulate themselves.80 During the small hours Chandler had finally tracked down the fault in Colossus (parasitic oscillations in some of the valves) and had fixed it by wiring in a few extra resistors.81 Flowers and his ‘band of brothers’ had met BP’s deadline—a deadline whose significance Flowers can only have guessed at.82
Less than a week later the Allied invasion of France began. The D-day landings of June 6 placed huge quantities of men and equipment on the beaches of Normandy. From the beachheads the Allies pushed their way into France through the heavy German defences. By mid-July the front had advanced only 20 or so miles inland, but by September Allied troops had swept across France and Belgium and were gathering close to the borders of Germany, on a front extending from Holland in the north to Switzerland in the south.83
Since the early months of 1944, Colossus I had been providing an unparalleled window on German preparations for the Allied invasion.84 Decrypts also revealed German appreciations of Allied intentions. Tunny messages supplied vital confirmation that the German planners were being taken in by Operation Fortitude, the extensive programme of deceptive measures designed to suggest that the invasion would come further north, in the Pas de Calais.85 In the weeks following the start of the invasion the Germans tightened Tunny security, instructing operators to change the patterns of the chi- and psi-wheels daily instead of monthly. Hand methods for discovering the new patterns were overwhelmed. With impeccable timing Colossus II’s device for breaking wheel patterns came to the rescue.
Once Flowers’ factory in Birmingham was properly up and running, new Colossi began arriving in the Newmanry at roughly six week intervals. Eventually three were dedicated to breaking wheel patterns.86 Flowers was a regular visitor at B.P. throughout the rest of 1944, overseeing the installation programme for the Mark 2 Colossi.87 By the end of the year seven Colossi were in operation. They provided the codebreakers with the capacity to find all twelve wheel settings by machine, and this was done in the case of a large proportion of decrypted messages.88 There were ten Colossi in operation by the time of the German surrender in 1945, and an eleventh was almost ready.
One of the most common misconceptions in the secondary literature is that Colossus was used against Enigma. Another is that Colossus was used against not Tunny but Sturgeon—an error promulgated by Brian Johnson’s influential televison series and accompanying book The Secret War.89 There are in fact many wild tales about Colossus in the history books. Georges Ifrah even states that Colossus produced English plaintext from the German ciphertext!90 As already explained, the output of Colossus was a series of counts indicating the correct wheel settings (or, later, the wheel patterns). Not even the de-chi was produced by Colossus itself, let alone the plaintext—and there was certainly no facility for the automatic translation of German into English.

‘At Bletchley Park, Alan Turing built a succession of vacuum-tube machines called Colossus that made mincemeat of Hitler’s Enigma codes’ (March 29, 1999).57
An insidious misconception concerns ownership of the inspiration for Colossus. Many accounts identify Turing as the key figure in the designing of Colossus. In a biographical article on Turing, the computer historian J. A. N. Lee said that Turing’s ‘influence on the development of Colossus is well known’,91 and in an article on Flowers, Lee referred to Colossus as ‘the cryptanalytical machine designed by Alan Turing and others’.92 Even a book on sale at the Bletchley Park Museum states that at Bletchley Park ‘Turing worked ... on what we now know was computer research’ which led to ‘the world’s first electronic, programmable computer, "Colossus"’.93

The view that Turing’s interest in electronics contributed to the inspiration for Colossus is indeed common. This claim is enshrined in codebreaking exhibits in leading museums; and in the Annals of the History of Computing Lee and Holtzman state that Turing ‘conceived of the construction and usage of high-speed electronic devices; these ideas were implemented as the "Colossus" machines’.94 However, the definitive 1945 General Report on Tunny makes matters perfectly clear: ‘Colossus was entirely the idea of Mr. Flowers’ (see the extract from page 35 in the right-hand column).95 By 1943 electronics had been Flowers’ driving passion for more than a decade and he needed no help from Turing. Turing was, in any case, away in the United States during the critical period at the beginning of 1943 when Flowers proposed his idea to Newman and worked out the design of Colossus on paper. Flowers emphasised in an interview that Turing ‘made no contribution’ to the design of Colossus.96 Flowers said: ‘I invented the Colossus. No one else was capable of doing it.’97
In his recent book on the history of computing, Martin Davis offers a garbled account of Colossus (see right-hand column). Here Davis conflates Turingery, which he calls ‘turingismus’, with Tutte’s statistical method. (ismus is a German suffix equivalent to the English ism. Newmanry codebreaker Michie explains the origin of Turingery’s slang name ‘Turingismus’: ‘three of us (Peter Ericsson, Peter Hilton and I) coined and used in playful style various fake-German slang terms for everything under the sun, including occasionally something encountered in the working environment. Turingismus was a case of the latter.’98) Turing’s method of wheel breaking from depths and Tutte’s method of wheel setting from non-depths were distant relatives, in that both used delta-ing. But there the similarity ended. Turingery, Tutte said, seemed to him ‘more artistic than mathematical’; in applying the method you had to rely on what ‘you felt in your bones’.99 Conflating the two methods, Davis erroneously concludes that Colossus was a physical embodiment of Turingery. But as explained above, Turingery was a hand method—it was Tutte’s method that ‘required the processing of lots of data’. Tutte’s method, not Turingery, was implemented in Heath Robinson and Colossus. ‘Turingery was not used in either breaking or setting by any valve machine of any kind’, Michie underlined.100

Sir Winston Churchill.60

ENIAC.61

GCHQ at Cheltenham.62

Architect’s model of GCHQ’s new doughnut-shaped building at Cheltenham.63

Jack Good.64

NSA Headquarters in Maryland.65

The Headquarters of the Government Code and Cypher School in Berkeley Street, London, in the 1920s.66


King’s College, Cambridge, birthplace of the universal Turing machine and the stored program concept.69

Turing was a founding father of modern computer science.71

John von Neumann.72



If Flowers could have patented the inventions that he contributed to the assault on Tunny, he would probably have become a very rich man. As it was, the personal costs that he incurred in the course of building the Colossi left his bank account overdrawn at the end of the war. Newman was offered an OBE for his contribution to the defeat of Germany, but he turned it down, remarking to ex-colleagues from Bletchley Park that he considered the offer derisory.101 Tutte received no public recognition for his vital work. Turing accepted an OBE, which he kept in his toolbox.
At the end of hostilities, orders were received from Churchill to break up the Colossi, and all involved with Colossus and the cracking of Tunny were gagged by the Official Secrets Act. The very existence of Colossus was to be classified indefinitely. Flowers described his reactions:
When after the war ended I was told that the secret of Colossus was to be kept indefinitely I was naturally disappointed. I was in no doubt, once it was a proven success, that Colossus was an historic breakthrough, and that publication would have made my name in scientific and engineering circles—a conviction confirmed by the reception accorded to ENIAC, the U.S. equivalent made public just after the war ended. I had to endure all the acclaim given to that enterprise without being able to disclose that I had anticipated it. What I lost in personal prestige, and the benefits which commonly accrue in such circumstances, can now only be imagined. But at the time I accepted the situation philosophically and, in the euphoria of a war that was won, lost any concern about what might happen in the future.102
ENIAC, commissioned by the U.S. army in 1943, was designed to calculate trajectories of artillery shells. Although not operational until the end of 1945—two years after Colossus first ran—ENIAC is standardly described as the first electronic digital computer. Flowers’ view of the ENIAC? It was just a number cruncher—Colossus, with its elaborate facilities for logical operations, was ‘much more of a computer than ENIAC’.103
The Newmanry’s Colossi might have passed into the public domain at the end of the fighting, to become, like ENIAC, the electronic muscle of a scientific research facility. The Newmanry’s engineers would quickly have adapted the equipment for peacetime applications. The story of computing might have unfolded rather differently with such a momentous push right at the beginning. Churchill’s order to destroy the Colossi was an almighty blow in the face for science—and for British industry.
In April 1946, codebreaking operations were transferred from Bletchley Park to buildings in Eastcote in suburban London.104 At the time of the move, the old name of the organisation, ‘Government Code and Cypher School’, was formally changed to ‘Government Communications Headquarters’ (GCHQ).105 Six years later another move commenced, and during 1952-54 GCHQ shifted its personnel and equipment, including its codebreaking machinery, away from the London area to a large site in Cheltenham.106 Some machines did survive the dissolution of the Newmanry. Two Colossi made the move from Bletchley Park to Eastcote, and then eventually on to Cheltenham.107 They were accompanied by two of the replica Tunny machines manufactured at Dollis Hill.108 One of the Colossi, known as ‘Colossus Blue’ at GCHQ, was dismantled in 1959 after fourteen years of postwar service. The remaining Colossus is believed to have stopped running in 1960.
During their later years the two Colossi were used extensively for training. Details of what they were used for prior to this remain classified. There is a hint of the importance of one new role for these Newmanry survivors in a letter written by Jack Good:
I heard that Churchill requested that all Colossi be destroyed after the war, but GCHQ decided to keep at least one of them. I know of that one because I used it myself. That was the first time it was used after the war. I used it for a purpose for which NSA [National Security Agency] were planning to build a new special-purpose machine. When I showed that the job could be carried out on Colossus, NSA decided not to go ahead with their plan. That presumably is one reason I am still held in high regard in NSA. Golde told me that one of his friends who visits NSA told Golde that I am ‘regarded as God’ there.109
After Bletchley’s own spectacular successes against the German machines, GCHQ was—not unnaturally—reluctant to use key-generating cipher machines to protect British high-grade diplomatic traffic. Instead GCHQ turned to one-time pad. Sender and receiver were issued with identical key in the form of a roll of teleprinter tape. This would be used for one message only. One-time pad is highly secure. The disadvantage is that a complex and highly efficient distribution network is required to supply users with key. It is probably true that GCHQ initially underestimated the difficulties of distributing key.
The GCHQ Colossi assisted in the production of one-time pad. Ex-Newmanry engineers used some of Flowers’ circuitry from Colossus to build a random noise generator able to produce random teleprinter characters on a punched tape. This device, code-named ‘Donald Duck’, exploited the random way in which electrons are emitted from a hot cathode. The tapes produced by Donald Duck were potential one-time pad. The tapes were checked by Colossus, and those that were not flat-random were weeded out. Newmanry-type tape-copying machines were used to make copies of tapes that passed the tests, and these were distributed to GCHQ’s clients.
Probably the Colossi had additional postwar applications. They may have been used to make character counts of enemy cipher traffic, searching for features that might give the cryptanalysts a purchase. Perhaps the GCHQ Colossi were even used against reconditioned German Tunny machines. Many Tunnies were captured by the invading British armies during the last stages of the war. If the National interest so dictated, Tunny machines may have been sold to commercial organisations or foreign powers, and the resulting traffic read by GCHQ.
Until the 1970s few had any idea that electronic computation had been used successfully during the Second World War. In 1975, the British government released a set of captioned photographs of the Colossi (several of which are reproduced above).110 By 1983, Flowers had received clearance to publish an account of the hardware of the first Colossus.111 Details of the later Colossi remained secret. So, even more importantly, did all information about how Flowers’ computing machinery was actually used by the codebreakers. Flowers was told by the British authorities that ‘the technical description of machines such as COLOSSUS may be disclosed’, but that he must not disclose any information about ‘the functions which they performed’.112 It was rather like being told that he could give a detailed technical description of the insides of a radar receiver, but must not say anything about what the equipment did (in the case of radar, reveal the location of planes, submarines, etc., by picking up radio waves bouncing off them). He was also allowed to describe some aspects of Tunny, but there was a blanket prohibition on saying anything at all relating to ‘the weaknesses which led to our successes’. In fact, a clandestine censor objected to parts of the account that Flowers wrote, and he was instructed to remove these prior to publication.113
There matters more or less stood until 1996, when the U.S. Government declassified some wartime documents describing the function of Colossus. These had been sent to Washington during the war by U.S. liaison officers stationed at Bletchley Park. The most important document remained classified, however: the 500 page General Report on Tunny written at Bletchley Park in 1945 by Jack Good, Donald Michie, and Geoffrey Timms. Thanks largely to Michie’s tireless campaigning, the report was declassified by the British Government in June 2000, finally ending the secrecy.
Colossus and the modern computer
As everyone who can operate a personal computer knows, the way to make the machine perform the task you want—word-processing, say—is to open the appropriate program stored in the computer’s memory. Life was not always so simple. Colossus did not store programs in its memory. To set up Colossus for a different job, it was necessary to modify some of the machine’s wiring by hand, using switches and plugs. The larger ENIAC was also programmed by re-routing cables and setting switches. The process was a nightmare: it could take the ENIAC’s operators up to three weeks to set up and debug a program.114 Colossus, ENIAC, and their like are called ‘program-controlled’ computers, in order to distinguish them from the modern ‘stored-program’ computer.
This basic principle of the modern computer, that is, controlling the machine’s operations by means of a program of coded instructions stored in the computer’s memory, was thought of by Turing in 1936. At the time, Turing was a shy, eccentric student at Cambridge University. His ‘universal computing machine’, as he called it—it would soon be known simply as the universal Turing machine—emerged from research that no-one would have guessed could have any practical application. Turing was working on a problem in mathematical logic, the so-called ‘decision problem’, which he learned of from lectures given by Newman. (For a description of the decision problem and Turing’s approach to it, see ‘Computable Numbers: A Guide’ in The Essential Turing.115) In the course of his attack on this problem, Turing thought up an abstract digital computing machine which, as he said, could compute ‘all numbers which could naturally be regarded as computable’.116 The universal Turing machine consists of a limitless memory in which both data and instructions are stored, in symbolically encoded form, and a scanner that moves back and forth through the memory, symbol by symbol, reading what it finds and writing further symbols. By inserting different programs into the memory, the machine can be made to carry out any algorithmic task. That is why Turing called the machine universal.
Turing’s fabulous idea was just this: a single machine of fixed structure that, by making use of coded instructions stored in memory, could change itself, chameleon-like, from a machine dedicated to one task into a machine dedicated to a completely different task—from calculator to word processor, for example. Nowadays, when many have a physical realisation of a universal Turing machine in their living room, this idea of a one-stop-shop computing machine is apt to seem as obvious as the wheel. But in 1936, when engineers thought in terms of building different machines for different purposes, the concept of the stored-program universal computer was revolutionary.
In 1936 the universal Turing machine existed only as an idea. Right from the start Turing was interested in the possibility of building such a machine, as to some extent was Newman, but before the war they knew of no practical way to construct a stored-program computer.117 It was not until the advent of Colossus that the dream of building an all-purpose electronic computing machine took hold of them. Flowers had established decisively and for the first time that large-scale electronic computing machinery was practicable, and soon after the end of the war Turing and Newman both embarked on separate projects to create a universal Turing machine in hardware. Racks of electronic components from the dismantled Colossi were shipped from Bletchley Park to Newman’s Computing Machine Laboratory at Manchester. Historians who did not know of Colossus tended to assume quite wrongly that Turing and Newman inherited their vision of an electronic computer from the ENIAC group in the U.S.
Even in the midst of the attack on Tunny, Newman was thinking about the universal Turing machine. He showed Flowers Turing’s 1936 paper about the universal machine, ‘On Computable Numbers’, with its key idea of storing symbolically encoded instructions in memory, but Flowers, not being a mathematical logician, ‘didn’t really understand much of it’.118 There is little doubt that by 1944 Newman had firmly in mind the possibility of building a universal Turing machine using electronic technology. It was just a question of waiting until he ‘got out’.119 In February 1946, a few months after his appointment to the University of Manchester, Newman wrote to the Hungarian-American mathematician von Neumann (like Newman considerably influenced by Turing’s 1936 paper, and himself playing a leading role in the post-ENIAC developments taking place in the U.S.):
I am ... hoping to embark on a computing machine section here, having got very interested in electronic devices of this kind during the last two or three years. By about eighteen months ago I had decided to try my hand at starting up a machine unit when I got out. ... I am of course in close touch with Turing.120
The implication of Flowers’ racks of electronic equipment was obvious to Turing too. Flowers said that once Colossus was in operation, it was just a matter of Turing’s waiting to see what opportunity might arise to put the idea of his universal computing machine into practice. (By the end of the war, Turing had educated himself thoroughly in electronic engineering: during the later part of the war he gave a series of evening lectures ‘on valve theory’.121) Turing’s opportunity came along in 1945, when John Womersley, head of the Mathematics Division of the National Physical Laboratory (NPL) in London, invited him to design and develop an electronic stored-program digital computer. Turing’s technical report ‘Proposed Electronic Calculator’,122 dating from the end of 1945 and containing his design for the ACE, was the first relatively complete specification of an electronic stored-program digital computer.123 The slightly earlier ‘First Draft of a Report on the EDVAC’,124 produced in about May 1945 by von Neumann, was much more abstract, saying little about programming, hardware details, or electronics. (The EDVAC, proposed successor to the ENIAC, was to be a stored-program machine. It was not fully working until 1952.125) Harry Huskey, the electronic engineer who subsequently drew up the first detailed hardware designs for the EDVAC, stated that the ‘information in the “First Draft” was of no help’.126 Turing, in contrast, supplied detailed circuit designs, full specifications of hardware units, specimen programs in machine code, and even an estimate of the cost of building the machine.
Turing asked Flowers to build the ACE, and in March 1946 Flowers said that a ‘minimal ACE’ would be ready by August or September of that year.127 Unfortunately, however, Dollis Hill was overwhelmed by a backlog of urgent work on the national telephone system, and it proved impossible to keep to Flowers’ timetable. In the end it was Newman’s team who, in June 1948, won the race to build the first stored-program computer. The first program, stored on the face of a cathode ray tube as a pattern of dots, was inserted manually, digit by digit, using a panel of switches. The news that the Manchester machine had run what was only a tiny program—just 17 instructions long—for a mathematically trivial task was ‘greeted with hilarity’ by Turing’s team working on the much more sophisticated ACE.128
A pilot model of the ACE ran its first program in May 1950. With an operating speed of 1 MHz, the pilot model ACE was for some time the fastest computer in the world. The pilot model was the basis for the very successful DEUCE computers, which became a cornerstone of the fledgling British computer industry—confounding the suggestion, made in 1946 by Sir Charles Darwin, Director of the NPL and grandson of the great Darwin, that ‘it is very possible that ... one machine would suffice to solve all the problems that are demanded of it from the whole country’.129
Appendix 1: The teleprinter alphabet
CONVENTIONAL NAME |
IMPULSE |
||||||
| 1 | 2 | 3 | 4 | 5 | IN LETTER SHIFT
|
IN FIGURE SHIFT
|
|
/ |
• | • | • | • | • | (no meaning) |
(no meaning) |
9 |
• | • | x | • | • | space | space |
H |
• | • | x | • | x | H | £ |
T |
• | • | • | • | x | T | 5 |
O |
• | • | • | x | x | O | 9 |
M |
• | • | x | x | x | M | full stop |
N |
• | • | x | x | • | N | comma |
3 |
• | • | • | x | • | carriage return | carriage return |
R |
• | x | • | x | • | R | 4 |
C |
• | x | x | x | • | C | colon |
V |
• | x | x | x | x | V | equals |
G |
• | x | • | x | x | G | @ |
L |
• | x | • | • | x | L | close bracket |
P |
• | x | x | • | x | P | 0 (zero) |
I |
• | x | x | • | x | I | 8 |
4 |
• | x | • | • | • | line feed | line feed |
A |
x | x | • | • | • | A | dash |
U |
x | x | x | • | • | U | 7 |
Q |
x | x | x | • | x | Q | 1 |
W |
x | x | • | • | x | W | 2 |
+ or 5 |
x | x | • | x | x | move to figure shift | (none) |
− or 8 |
x | x | x | x | x | (none) | move to letter shift |
K |
x | x | x | x | • | K | open bracket |
J |
x | x | • | x | • | J | ring bell |
D |
x | • | • | x | • | D | who are you? |
F |
x | • | x | x | • | F | per cent |
X |
x | • | x | x | x | X | / |
B |
x | • | • | x | x | B | ? |
Z |
x | • | • | • | x | Z | + |
Y |
x | • | x | • | x | Y | 6 |
S |
x | • | x | • | • | S | apostrophe |
E |
x | • | • | • | • | E | 3 |
In teleprinter code the letters most frequently used are represented by the fewest holes in the tape, which is to say by the fewest crosses, in B.P. notation.130 For instance E, the commonest letter of English, is x••••, and T, the next most frequent, is ••••x. The table in the right-hand column gives the 5-bit teleprinter code for each character of the teleprint alphabet.
The left-hand column of the table shows the characters of the teleprint alphabet as they would have been written down by the Bletchley codebreakers. For example, the codebreakers wrote ‘9’ to indicate a space (as in ‘to9indicate’) and ‘3’ to indicate a carriage return.
The ‘move to figure shift’ character (which some at Bletchley wrote as ‘+’ and some as ‘5’) told the teleprinter to shift from printing letters to printing figures; and the ‘move to letter shift’ character (written ‘−’ or ‘8’) told the machine to shift from printing figures to printing letters. With the teleprinter in letter mode, the keys along the top row of the keyboard would print QWERTYUIOP, and in figure mode the same keys would print 1234567890.
Most of the keyboard characters had different meanings in letter mode and figure mode. In figure mode the M-key printed a full stop, the N-key a comma, the C-key a colon, and the A-key a dash, for example. (Unlike a modern keyboard, the teleprinter did not have separate keys for punctuation.) The meanings of the other keys in figure mode are given at the right of the table.
To cause the teleprinter to print 123 WHO, ME? the operator must first press figure shift and key Q W E to produce the numbers. He or she then drops into letter mode and keys a space (or vice versa), followed by W H O. To produce the comma it is necessary to press figure shift then N. This is followed by letter shift, space, and M E. A final figure shift followed by B produces the question mark.
+QWE−9WHO+N−9ME+B
Often Tunny operators would repeat the figure-shift and letter-shift characters, sending a comma as ++N−− and a full stop as ++M−−, for example. Following this practice, the operator would key
++QWE−−9WHO++N−−9ME++B
Presumably the shift characters were repeated to ensure that the shift had ‘taken’. These repetitions were very helpful to the British, since a correct guess at a punctuation mark could yield six characters of text (including the trailing 9).
Appendix 2: The Tunny encipherment equation and Tutte’s 1 + 2 break-in
First, some notation. P is the plaintext, C is the cipher text, χ is the stream of letters contributed to the message’s key by the chi-wheels, and Ψ is the stream contributed by the psi-wheels. χ + Ψ is the result of adding χ and Ψ using the rules of Tunny-addition. ΔC is the result of delta-ing the ciphertext, Δ(χ + Ψ) is the result of delta-ing the stream of characters that results from adding χ and Ψ, and so forth.
Since C is produced by adding the key to P, and the key is produced by adding χ and Ψ, the fundamental encipherment equation for the Tunny machine is:
C = P + χ + Ψ
C1 is written for the first impulse of C (i.e. the first of the five streams in the teleprint representation of the ciphertext); and similarly P1, χ1 and Ψ1 are the first impulses of P, χ and Ψ respectively. The encipherment equation for the first impulse is:
C1 = P1 + χ1 + Ψ1
Delta-ing each side of this equation gives
ΔC1 = Δ(P1 + χ1 + Ψ1)
Delta-ing the sum of two or more impulses produces the same result as first delta-ing each impulse and then summing. So
ΔC1 = ΔP1 + Δχ1 + ΔΨ1
Likewise for the second impulse:
ΔC2 = ΔP2 + Δχ2 + ΔΨ2
Adding the equations for the first and second impulses gives
ΔC1 + ΔC2 = ΔP1 + ΔP2 + Δχ1 + Δχ2 + ΔΨ1 + ΔΨ2
which is the same as
Δ(C1 + C2) = Δ(P1 + P2) + Δ(χ1 + χ2) + Δ(Ψ1 + Ψ2)
Because of the staggering motion of the psi-wheels, Δ(Ψ1 + Ψ2) turns out to be about 70% dot. But adding dot leaves you where you started: cross plus dot is dot and dot plus dot is dot. It follows that the addition of Δ(Ψ1 + Ψ2) more often than not has no effect. So
Δ(C1 + C2) = Δ(P1 + P2) + Δ(χ1 + χ2)
is true more often than not.
Tutte also discovered that Δ(P1 + P2) is approximately 60% dot. This effect is the result of various factors, for instance the Tunny operators’ habit of repeating certain characters (see Appendix 1), and contingencies of the way the individual letters are represented in the underlying teleprinter code—for example, the delta of the sum of the first and second impulses of the common bigram (or letter pair) DE is dot, as it is for other common bigrams such as BE, ZE, ES. So it is true more often than not that
Δ(C1 + C2) = Δ(χ1 + χ2)
Tutte’s ‘1 + 2 break in’ is this. Δ(C1 + C2) is stepped through the delta-ed sum of the first and second impulses of the entire stream of characters from the chi-wheels. Generally the correspondence between Δ(C1 + C2) and a strip from the delta-ed chi of the same length will be no better than chance. If, however, Δ(C1 + C2) and a strip of delta-ed chi correspond more often than not, then a candidate has been found for Δ(χ1 + χ2), and so for the first two impulses of χ. The greater the correspondence, the likelier the candidate.131
References
[1] Bauer, F. L. 2006 ‘The Tiltman Break’, in [10].
[2] Cairncross, J. 1997 The Enigma Spy: The Story of the Man who Changed the Course of World War Two, London: Century.
[3] Campbell-Kelly, M. 2005 ‘The ACE and the Shaping of British Computing’, in [9].
[4] Chandler, W. W. 1983 ‘The Maintenance and Installation of Colossus’, Annals of the History of Computing, vol. 5, pp. 260-2.
[5] Coombs, A. W. M. 1983 ‘The Making of Colossus’, Annals of the History of Computing, vol. 5, pp. 253-9.
[6] Copeland, B. J. (ed.) 2004 The Essential Turing, Oxford: Oxford University Press.
[7] Copeland, B. J. 2004 ‘Computable Numbers: A Guide’, in [6].
[8] Copeland, B. J. 2004 ‘Enigma’, in [6].
[9] Copeland, B. J. (ed.) 2005 Alan Turing’s Automatic Computing Engine: The Master Codebreaker’s Struggle to Build the Modern Computer, Oxford: Oxford University Press.
[10] Copeland, B. J. et al. 2010 Colossus: The Secrets of Bletchley Park’s Codebreaking Computers (2nd edition), Oxford: Oxford University Press.
[11] Davies, D. 1995 ‘The Lorenz Cipher Machine SZ42’, Cryptologia, vol. 19, pp. 517-39.
[12] Davis, M. 2000 The Universal Computer: The Road from Leibniz to Turing, New York: Norton.
[13] de Bruyne, N. A., Webster, H. C. 1931 ‘Note on the Use of a Thyratron with a Geiger Counter’, Proceedings of the Cambridge Philosophical Society, vol. 27, pp. 113-15.
[14] Enever, E. 1994 Britain’s Best Kept Secret: Ultra’s Base at Bletchley Park (2nd edition), Stroud: Alan Sutton.
[15] Erskine, R., Freeman, P. 2003 ‘Brigadier John Tiltman: One of Britain’s Finest Cryptologists’, Cryptologia, vol. 27, pp. 289-318.
[16] Flowers, T. H. 1983 ‘The Design of Colossus’, Annals of the History of Computing, vol. 5, pp. 239-52.
[17] Flowers, T. H. 2006 ‘D-Day at Bletchley Park’, in [10].
[18] Golden, F. 1999 ‘Who Built the First Computer?’, Time, March 29, 1999, no. 13, p. 82.
[19] Hinsley, F. H. et al. 1981 British Intelligence in the Second World War, Vol. 2, London: Her Majesty’s Stationery Office.
[20] Hinsley, F. H. et al. 1988 British Intelligence in the Second World War, Vol. 3, Part 2, London: Her Majesty’s Stationery Office.
[21] Hinsley, H. 1996 ‘The Counterfactual History of No Ultra’, Cryptologia, vol. 20, pp. 308-24.
[22] Hull, A. W. 1929 ‘Hot-cathode Thyratrons’, General Electric Review, vol. 32, pp. 390-99.
[23] Huskey, H. D. 1972 ‘The Development of Automatic Computing’, in Proceedings of the First USA-JAPAN Computer Conference, Tokyo.
[24] Ifrah, G. 2001 The Universal History of Computing: From the Abacus to the Quantum Computer, New York: John Wiley.
[25] Johnson, B. 1978 The Secret War, London: British Broadcasting Corporation.
[26] Lee, J. A. N. 1995 Computer Pioneers, Los Alamitos: IEEE Computer Society Press.
[27] Lee, J. A. N., Holtzman, G. 1999 ‘50 Years After Breaking the Codes’, Annals of the History of Computing, vol. 17, pp. 32-43.
[28] McCorduck, P. 1979 Machines Who Think, New York: W. H. Freeman.
[29] Murray, D. (no date) Murray Multiplex: Technical Instructions, Manual no. 1: General Theory, Croydon: Creed and Coy.
[30] Stern, N. 1981 From ENIAC to UNIVAC: An Appraisal of the Eckert-Mauchly Computers, Bedford, Mass.: Digital Press.
[31] Turing, A. M. 1936 ‘On Computable Numbers, with an Application to the Entscheidungsproblem’, Proceedings of the London Mathematical Society, Series 2, vol. 42 (1936-7), pp. 230-65. Reprinted in [6].
[32] Turing, S. 1959 Alan M. Turing, Cambridge: W. Heffer.
[33] Tutte, W. T. 2006 ‘My Work at Bletchley Park’, in [10].
[34] Weierud, F. 2006 ‘Bletchley Park’s Sturgeon—The Fish That Laid No Eggs’, in [10].
[35] Wynn-Williams, C. E. 1931 ‘The Use of Thyratrons for High Speed Automatic Counting of Physical Phenomena’, Proceedings of the Royal Society, Series A, vol. 132, pp. 295-310.
[36] Wynn-Williams, C. E. 1932 ‘A Thyratron Scale of Two Automatic Counter’, Proceedings of the Royal Society of London, Series A, vol. 136, pp. 312-24.
Notes
1 The physical Tunny machine is described in section 11 of General Report on Tunny, and in Davies [11]. The machine’s function and use is described in sections 11 and 94 of General Report on Tunny. General Report on Tunny was written at Bletchley Park in 1945 by Tunny-breakers Jack Good, Donald Michie and Geoffrey Timms; it was released by the British government in 2000 to the National Archives/Public Record Office (PRO) at Kew (document reference HW 25/4 (vol. 1), HW 25/5 (vol. 2)). A digital facsimile is available in The Turing Archive for the History of Computing http://www.AlanTuring.net/tunny_report.
2 Bletchley’s work on Sturgeon is described in Weirud's ‘Bletchley Park's Sturgeon, the Fish that Laid No Eggs’ in a previous issue of this journal.
3 On Thrasher, see section 93 of General Report on Tunny.
4 See Copeland [14], ch. 7.
5 General Report on Tunny, p. 14. General Report on Tunny mentions that the first messages on the experimental link passed between Vienna and Athens (p. 297).
6 General Report on Tunny, p. 320.
7 General Report on Tunny, pp. 14, 320, 458.
8 General Report on Tunny, p. 14.
9 General Report on Tunny, p. 14.
10 General Report on Tunny, p. 395.
11 General Report on Tunny, p. 15.
12 General Report on Tunny, p. 15.
13 General Report on Tunny, p. 5.
14 General Report on Tunny, p. 4.
15 General Report on Tunny, p. 5.
16 British message reference number CX/MSS/2499/T14; PRO reference HW1/1648. Words enclosed in square brackets do not appear in the original. (Thanks to Ralph Erskine for assistance in locating this document. An inaccurate version of the intercept appears in Hinsley [19], pp. 764-5.)
17 Copy of message CX/MSS/2499/T14, PRO document reference HW5/242, p. 4.
18 ‘A Postponed German Offensive (Operations ZITADELLE and EULE)’ (anon., Government Code and Cypher School, 7 June 1943; PRO reference HW13/53), p. 2.
19 Documents from G.C. & C.S. to Churchill, 30 April 1943 (PRO reference HW1/1648). An earlier decrypt concerning Zitadelle (13 April 1943), and an accompanying note from ‘C’ to Churchill, are at HW1/1606.
20 Tape-recorded interview with Harry Hinsley (Sound Archive, Imperial War Museum, London (reference number 13523)).
21 Cairncross [2], p. 98, Hinsley [21], pp. 322-3, interview with Hinsley (see above).
22 Hinsley [19], p. 626.
23 Hinsley [19], p. 625.
24 Hinsley [19], p. 627.
25 Hinsley [19], p. 627.
26 Newman in interview with Christopher Evans (‘The Pioneers of Computing: An Oral History of Computing’ (London: Science Museum)).
27 Erskine and Freeman [15].
28 For further information on Turing, see Copeland The Essential Turing and Colossus: The Secrets of Bletchley Park’s Codebreaking Computers.
29 Bauer [1], p. 372.
30 Tutte [33], pp. 359-630.
31 See Copeland The Essential Turing.
32 Good in interview with Pamela McCorduck (McCorduck [28], p. 53).
33 General Report on Tunny, p. 313.
34 General Report on Tunny, p. 28.
35 General Report on Tunny, p. 28.
36 General Report on Tunny, pp. 28, 320-2.
37 Newman in interview with Evans.
38 Wynn-Williams [35], [36]; see also Hull [22], de Bruyne & Webster [13].
39 General Report on Tunny, p. 22.
40 General Report on Tunny, p. 20.
41 Letter from Harry Fensom to Copeland (4 May 2001).
42 General Report on Tunny, p. 328.
43 Newman in interview with Evans.
44 General Report on Tunny, p. 328.
45 Unless indicated otherwise, material in this chapter relating directly to Flowers derives from (1) Flowers in interviews with Copeland, 1996-1998 (2) Flowers in interview with Christopher Evans in 1977 (‘The Pioneers of Computing: an Oral History of Computing’, London: Science Museum).
46 Flowers in interview with Copeland (July 1996).
47 Flowers in interview with Copeland (July 1998).
48 Flowers in interview with Copeland (July 1996); General Report on Tunny, p. 33.
49 Flowers in interview with Copeland (July 1996); Flowers [16], p. 244.
50 Flowers, T. H. ‘Colossus – Origin and Principles’, typescript, no date, p. 3; Coombs in interview with Christopher Evans in 1976 (‘The Pioneers of Computing: An Oral History of Computing’ (London: Science Museum)). ‘Incredulity’ is Flowers’ word.
51 Flowers, ‘Colossus – Origin and Principles’, p. 3.
52 Flowers in interview with Copeland (July 1996).
53 Ibid.
54 Ibid.
55 Flowers, ‘Colossus – Origin and Principles’, p. 3.
56 Myers, K. ‘Dollis Hill and Station X’, in The Turing Archive for the History of Computing http://www.AlanTuring.net/myers.
57 General Report on Tunny, p. 35.
58 Flowers in interview with Evans (© Board of Trustees of the Science Museum).
59 Flowers [16], p. 245; Flowers in interview with Evans.
60 Flowers in interview with Copeland (July 1996); Flowers in interview with Darlow Smithson (no date); Flowers in interview with staff of the Imperial War Museum, London (1998).
61 Newman, M. H. A. ‘Report on Progress’ (Newmanry, 18 January 1944; PRO document reference HW14/96), p. 4.
62 Letter from Fensom to Copeland (18 August 2005).
63 General Report on Tunny, p. 35.
64 General Report on Tunny, p. 34.
65 General Report on Tunny, p. 28.
66 General Report on Tunny, p. 35.
67 Flowers [16], p. 246.
68 Flowers [16], p. 245.
69 Flowers [16], p. 246.
70 Flowers in interview with Copeland (July 1996).
71 Note from Donald Michie to Copeland (27 May 2002), reporting a disclosure by Coombs in the 1960s.
72 General Report on Tunny, p. 461.
73 Flowers’ personal diary, 4 May 1944.
74 Ibid.
75 Chandler [4], p. 261.
76 Flowers [16], p. 246.
77 Flowers’ personal diary, 31 May 1944.
78 Letter from Chandler to Brian Randell, 24 January 1976; unpublished manuscript by Gil Hayward ‘1944 - 1946’ (2002).
79 Flowers’ personal diary, 1 June 1944.
80 Hayward, ‘1944 - 1946’.
81 Flowers [16], p. 247.
82 Coombs [5], p. 259.
83 Hinsley [20]: maps ‘OVERLORD’ (frontispiece) and ’September position 1944’ (facing p. 365).
84 Some crucial decrypts are listed by Hinsley [20], ch. 44 and appendix 10.
85 Hinsley [20], pp. 47-65.
86 General Report on Tunny, p. 36.
87 Flowers’ personal diary for 1944.
88 General Report on Tunny, p. 35.
89 Johnson [25], pp. 339-47.
90 Ifrah [24], p. 218.
91 Lee [26], p. 671.
92 Lee [26], p. 306.
93 Enever [14], pp. 36-7.
94 Lee and Holtzman [27], p. 33.
95 General Report on Tunny, p. 35.
96 Flowers in interview with Copeland (July 1996).
97 Flowers in interview with Copeland (July 1996).
98 Letter from Michie to Copeland (29 July 2001).
99 Tutte [33], p. 360.
100 Letter from Michie to Copeland (28 November 2001).
101 Peter Hilton in interview with Copeland (May 2001).
102 Flowers [17], pp. 82-3.
103 Flowers in interview with Copeland (July 1996).
104 Freeman, P. ‘How GCHQ Came to Cheltenham’ (undated, GCHQ), p. 8.
105 Ibid.
106 Freeman, ‘How GCHQ Came to Cheltenham’, p. 30.
107 Unpublished manuscript by Gil Hayward (2002).
108 Ibid.
109 Letter from Jack Good to Henry H. Bauer (2 January 2005).
110 The photographs were released to the Public Record Office (PRO reference FO 850/234).
111 Flowers [16].
112 Personal files of T. H. Flowers (24 May 1976, 3 September 1981).
113 Personal files of T. H. Flowers (3 September 1981).
114 Campbell-Kelly [3], p. 151.
115 Copeland [7], pp. 45-53.
116 Turing [31], p. 249.
117 Newman in interview with Evans.
118 Flowers in interview with Copeland (July 1996).
119 Letter from Newman to von Neumann (8 February 1946) (in the von Neumann Archive at the Library of Congress, Washington, D.C.; a digital facsimile is in The Turing Archive for the History of Computing http://www.AlanTuring.net/newman_vonneumann_8feb46).
120 Ibid.
121 Turing [32], p. 74.
122 In Copeland [9].
123 A digital facsimile of the original typewritten report is in The Turing Archive for the History of Computing http://www.AlanTuring.net/proposed_electronic_calculator.
124 In Stern [30].
125 Huskey [23], p. 702.
126 Letter from Huskey to Copeland (4 February 2002).
127 ’Status of the Delay Line Computing Machine at the P.O. Research Station’ (anon., National Physical Laboratory, 7 March 1946; in the Woodger Papers (catalogue reference M12/105); a digital facsimile is in The Turing Archive for the History of Computing http://www.AlanTuring.net/delay_line_status).
128 Michael Woodger in interview with Copeland (June 1998).
129 Darwin, C. ‘Automatic Computing Engine (ACE)’ (National Physical Laboratory, 17 April 1946; PRO document reference DSIR 10/275); a digital facsimile is in The Turing Archive for the History of Computing http://www.AlanTuring.net/darwin_ace).
130 In Murray [29].
131 This article is a revised and illustrated version of Copeland, B.J. ‘Breaking the Lorenz Schlüsselzusatz Traffic’, in de Leeuw, K., Bergstra, J. (eds) The History of Information Security: A Comprehensive Handbook (Amsterdam: Elsevier Science, 2007), pp. 447-477.
Illustration credits
- 1 Photo by Duncan Shaw-Brown
- 2 Source: General Report on Tunny; Crown copyright, National Archives Image Library, Kew. Reproduced from Copeland, B.J. Colossus: The Secrets of Bletchley Park’s Codebreaking Computers (Oxford: Oxford University Press, 2010). Photo enhanced by Dustin Barrett and Parker Bright
- 3 Recreated from damaged archival photographs by Jack Copeland and Dustin Barrett. Reproduced from Copeland, B.J. Colossus: The Secrets of Bletchley Park’s Codebreaking Computers (Oxford: Oxford University Press, 2010)
- 4 Source: Science and Society Picture Library, National Museum of Science and Industry, London
- 5 Reproduced from Copeland, B.J. Colossus: The Secrets of Bletchley Park’s Codebreaking Computers (Oxford: Oxford University Press, 2010), p. 38
- 6 Reproduced from Copeland, B.J. Colossus: The Secrets of Bletchley Park’s Codebreaking Computers (Oxford: Oxford University Press, 2010), p. 38
- 7 Map by Dustin Barrett and Jack Copeland. Reproduced from Copeland, B.J. Colossus: The Secrets of Bletchley Park’s Codebreaking Computers (Oxford: Oxford University Press, 2010), p. 41
- 8 Source: Bletchley Park Trust. Photo enhanced by Parker Bright
- 9 Source: General Report on Tunny; Crown copyright, National Archives Image Library, Kew. Reproduced from Copeland, B.J. Colossus: The Secrets of Bletchley Park’s Codebreaking Computers (Oxford: Oxford University Press, 2010). Photo enhanced by Parker Bright
- 10 Recreated from a damaged family photograph by Jack Copeland and Dustin Barrett. Reproduced from Copeland, B.J. Colossus: The Secrets of Bletchley Park’s Codebreaking Computers (Oxford: Oxford University Press, 2010)
- 11 Source: Picture Library, Imperial War Museum, London. Photo enhanced by Dustin Barrett
- 12 Reproduced from Copeland, B.J. Colossus: The Secrets of Bletchley Park’s Codebreaking Computers (Oxford: Oxford University Press, 2010), p. 47
- 13 Satellite image courtesy of Google Maps
- 14 Reproduced from Copeland, B.J. Colossus: The Secrets of Bletchley Park’s Codebreaking Computers (Oxford: Oxford University Press, 2010), pp. 5-6
- 15 Source: Bletchley Park Trust. Photo enhanced by Parker Bright
- 16 Source: William Newman
- 17 Source: Barbara Eachus and Government Communications Headquarters, Cheltenham. Photo enhanced by Parker Bright
- 18 Source: Beryl Turing and King's College Library, Cambridge. Photo enhanced by Dustin Barrett and Parker Bright
- 19 Source: William Tutte. Photo enhanced by Dustin Barrett and Parker Bright
- 20 Source: Bletchley Park Trust. Reproduced from Bauer, F.L. ‘The Tiltman Break’, in Copeland, B.J. Colossus: The Secrets of Bletchley Park’s Codebreaking Computers (Oxford: Oxford University Press, 2010), p. 370
- 21 Reproduced from Bauer, F.L. ‘The Tiltman Break’, in Copeland, B.J. Colossus: The Secrets of Bletchley Park’s Codebreaking Computers (Oxford: Oxford University Press, 2010), p. 372
- 22 Source: William Tutte. Photo enhanced by Parker Bright
- 23 Source: Beryl Turing and King's College Library, Cambridge. Photo enhanced by Parker Bright
- 24 Recreated by Jack Copeland and Dustin Barrett from a wartime photograph held by the Picture Library, Imperial War Museum, London
- 25 Reproduced from Copeland, B.J. Colossus: The Secrets of Bletchley Park’s Codebreaking Computers (Oxford: Oxford University Press, 2010), p. 67
- 26 Source: Beryl Turing and King's College Library, Cambridge. Photo enhanced by Jack Copeland, Dustin Barrett and Parker Bright
- 27 Source: Karin Dawe. Photo enhanced by Parker Bright
- 28 Source: William Newman
- 29 Source: General Report on Tunny; Crown copyright, National Archives Image Library, Kew. Reproduced from Copeland, B.J. Colossus: The Secrets of Bletchley Park’s Codebreaking Computers (Oxford: Oxford University Press, 2010). Photo enhanced by Dustin Barrett and Parker Bright
- 30 Source: General Report on Tunny; Crown copyright, National Archives Image Library, Kew. Reproduced from Copeland, B.J. Colossus: The Secrets of Bletchley Park’s Codebreaking Computers (Oxford: Oxford University Press, 2010). Photo enhanced by Dustin Barrett and Parker Bright
- 31 Source: Government Communication Headquarters, Cheltenham. Photo enhanced by Jack Copeland and Dustin Barrett
- 32 Source: Jerry Roberts. Photo enhanced by Dustin Barrett and Parker Bright
- 33 Reproduced from Copeland, B.J. Colossus: The Secrets of Bletchley Park’s Codebreaking Computers (Oxford: Oxford University Press, 2010), p. 70
- 34 Source: William Tutte. Photo enhanced by Parker Bright
- 35 Source: General Report on Tunny; Crown copyright, National Archives Image Library, Kew. Reproduced from Copeland, B.J. Colossus: The Secrets of Bletchley Park’s Codebreaking Computers (Oxford: Oxford University Press, 2010). Photo enhanced by Jack Copeland, Dustin Barrett and Parker Bright
- 36 Source: Rowe, A. P. One Story of Radar (Cambridge: Cambridge University Press, 1948). Photo enhanced by Parker Bright
- 37 Source: National Physical Laboratory, Teddington (Crown copyright). Photo enhanced by Parker Bright
- 38 Source: Flowers, T.H. ‘Colossus’, in Copeland, B.J. Colossus: The Secrets of Bletchley Park’s Codebreaking Computers (Oxford: Oxford University Press, 2010), p. 92
- 39 Source: General Report on Tunny; Crown copyright, National Archives Image Library, Kew. Reproduced from Copeland, B.J. Colossus: The Secrets of Bletchley Park’s Codebreaking Computers (Oxford: Oxford University Press, 2010). Photo enhanced by Jack Copeland and Dustin Barrett
- 40 Photo by Jack Copeland
- 41 Source: Turing, S. Alan M. Turing (Cambridge: W. Heffer, 1959). Reproduced by permission of Heffers Bookshop (Cambridge)
- 42 Source: National Archives and Records Administration, College Park, Maryland, USA. Photo enhanced by Jack Copeland and Dustin Barrett
- 43 Source: General Report on Tunny; Crown copyright, National Archives Image Library, Kew. Reproduced from Copeland, B.J. Colossus: The Secrets of Bletchley Park’s Codebreaking Computers (Oxford: Oxford University Press, 2010). Photo enhanced by Jack Copeland and Dustin Barrett
- 44 Source: General Report on Tunny; Crown copyright, National Archives Image Library, Kew. Reproduced from Copeland, B.J. Colossus: The Secrets of Bletchley Park’s Codebreaking Computers (Oxford: Oxford University Press, 2010). Photo enhanced by Jack Copeland and Dustin Barrett
- 45 Source: Flowers, T.H. ‘Colossus’, in Copeland, B.J. Colossus: The Secrets of Bletchley Park’s Codebreaking Computers (Oxford: Oxford University Press, 2010), p. 96
- 46 Image enhanced by Parker Bright
- 47 Image enhanced by Parker Bright
- 48 Source: General Report on Tunny; Crown copyright, National Archives Image Library, Kew. Reproduced from Copeland, B.J. Colossus: The Secrets of Bletchley Park’s Codebreaking Computers (Oxford: Oxford University Press, 2010). Photo enhanced by Jack Copeland and Dustin Barrett
- 49 Source: General Report on Tunny; Crown copyright, National Archives Image Library, Kew. Reproduced from Copeland, B.J. Colossus: The Secrets of Bletchley Park’s Codebreaking Computers (Oxford: Oxford University Press, 2010). Photo enhanced by Jack Copeland and Dustin Barrett
- 50 Source: Donald Michie. Photo enhanced by Jack Copeland, Dustin Barrett and Parker Bright
- 51 Source: Bill Chandler and Brian Randell
- 52 Source: U.S. Library of Congress. Map modified by Parker Bright
- 53 Source: Army Signal Corps Collection, National Archives and Records Administration, College Park, Maryland, USA
- 54 Photo by Charles Turner
- 55 Source: Frode Weierud. Reproduced from Copeland, B.J. Colossus: The Secrets of Bletchley Park’s Codebreaking Computers (Oxford: Oxford University Press, 2010)
- 56 Lee [26], p. 492
- 57 Golden, F. ‘Who Built the First Computer?’, Time, March 29, 1999, no. 13, p. 82. Cover: http://www.time.com/time/covers/0,16641,19990329,00.html
- 58 Crown copyright, National Archives, Kew. http://www.AlanTuring.net/tunny_report/
- 59 Davis [12], pp. 174-175
- 60 Source: Canada Science and Technology Museum / Musée des sciences et de la technologie du Canada. http://www.flickr.com/photos/cstm-mstc/; license: CC BY-NC-ND 2.0
- 61 Source: Collections of the University of Pennsylvania Archive
- 62 Source: Government Communications Headquarters
- 63 Source: http://www.flickr.com/photos/senselessviolets/; license: CC BY-NC 2.0
- 64 Source: Jack Good. Photo enhanced by Dustin Barrett and Parker Bright
- 65 Source: National Security Agency. http://www.nsa.gov/about/_images/pg_hi_res/nsa_aerial.jpg
- 66 Source: Government Communications Headquarters
- 67 Crown copyright, National Archives, Kew
- 68 Crown copyright, National Archives, Kew
- 69 Source: Andrew Pearce, © Fotogenix.co.uk
- 70 Source: Copeland, B.J. (ed.) The Essential Turing (Oxford: Oxford University Press, 2004), p.7
- 71 Source: Beryl Turing and King's College Library, Cambridge
- 72 Source: Archives of the Institute for Advanced Study, Princeton; photo by Alan Richards
- 73 Source: http://www.AlanTuring.net/proposed_electronic_calculator
- 74 Source: School of Computer Science, University of Manchester. Photo enhanced by Parker Bright
- 75 Source: National Physical Laboratory, Teddington (Crown copyright). Photo enhanced by Jack Copeland and Dustin Barrett
- 76 Reproduced from Copeland, B.J. Colossus: The Secrets of Bletchley Park’s Codebreaking Computers (Oxford: Oxford University Press, 2010), p. 349